题目内容
10．在菱形ABCD中，若对角线长AC=3cm，BD=4cm，则它的面积是6cm2．分析 根据菱形的对角线的长度即可直接计算菱形ABCD的面积．
解答 解：∵菱形的对角线长AC、BD的长度分别为3cm，4cm，
∴菱形ABCD的面积S=$\frac{1}{2}$BD•AC=$\frac{1}{2}$×3×4=6cm2．
故答案为：6．
点评 本题考查了菱形对角线互相平分的性质，本题中菱形ABCD的面积等于对角线乘积的一半是解题的关键．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
1．
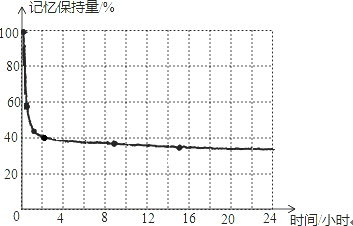德国心理学家艾宾浩斯（H．Ebbinghaus）研究发现，遗忘在学习之后立即开始，而且遗忘的进程并不是均匀的．最初遗忘速度很快，以后逐渐缓慢．他认为“记忆保持量是时间的函数”，他用无意义音节（由若干音节字母组成、能够读出、但无内容意义即不是词的音节）作记忆材料，用节省法计算保持和遗忘的数量．他通过测试，得到了一些数据如下表，然后又根据这些数据绘出了一条曲线，即著名的艾宾浩斯记忆遗忘曲线，如下图．该曲线对人类记忆认知研究产生了重大影响．
观察图象及表格，回答下列问题：
（1）2小时后，记忆保持量大约是多少？
（2）说明图中点A的坐标表示的实际意义．
（3）你从记忆遗忘曲线中还能获得什么信息？写出一条即可．
德国心理学家艾宾浩斯（H．Ebbinghaus）研究发现，遗忘在学习之后立即开始，而且遗忘的进程并不是均匀的．最初遗忘速度很快，以后逐渐缓慢．他认为“记忆保持量是时间的函数”，他用无意义音节（由若干音节字母组成、能够读出、但无内容意义即不是词的音节）作记忆材料，用节省法计算保持和遗忘的数量．他通过测试，得到了一些数据如下表，然后又根据这些数据绘出了一条曲线，即著名的艾宾浩斯记忆遗忘曲线，如下图．该曲线对人类记忆认知研究产生了重大影响．| 时间间隔 | 记忆保持量 |
| 刚记完 | 100% |
| 20分钟后 | 58.2% |
| 1小时后 | 44.2% |
| 8～9小时后 | 35.8% |
| 1天后 | 33.7% |
| 2天后 | 27.8% |
| 6天后 | 25.4% |
（1）2小时后，记忆保持量大约是多少？
（2）说明图中点A的坐标表示的实际意义．
（3）你从记忆遗忘曲线中还能获得什么信息？写出一条即可．
18．已知方程组$\left\{\begin{array}{l}{bx+ay=3}\\{ax-by=-1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$，求a，b的值（ ）
| A． | $\left\{\begin{array}{l}{a=1}\\{b=1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$ |
5．下列四个命题：
（1）若直角三角形的两条边长为5和12，则第三边长是13；
（2）如果a≥0，那么${（\sqrt{a}）^2}$=a；
（3）若点P（a，b）在第三象限，则点P（-a，-b+1）在第一象限；
（4）“对顶角相等”没有逆定理；
其中假命题有（ ）
（1）若直角三角形的两条边长为5和12，则第三边长是13；
（2）如果a≥0，那么${（\sqrt{a}）^2}$=a；
（3）若点P（a，b）在第三象限，则点P（-a，-b+1）在第一象限；
（4）“对顶角相等”没有逆定理；
其中假命题有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
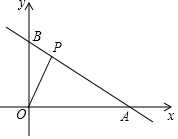直线y=kx+6与x轴、y轴分别交于A、B两点，点A的坐标为（8，0）．
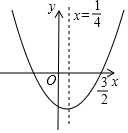如图，已知二次函数y=ax2+bx+c的图象如图所示，则下列四个结论：①a+b+c＜0；②a+c=b；③b=-2a；④4ac-b2＜0，其中正确的结论有（ ）