题目内容
20.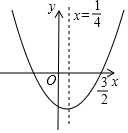 如图,已知二次函数y=ax2+bx+c的图象如图所示,则下列四个结论:①a+b+c<0;②a+c=b;③b=-2a;④4ac-b2<0,其中正确的结论有( )
如图,已知二次函数y=ax2+bx+c的图象如图所示,则下列四个结论:①a+b+c<0;②a+c=b;③b=-2a;④4ac-b2<0,其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 先充分挖掘图象所给出的信息,包括对称轴、开口方向、与坐标轴的交点、顶点位置等,然后根据二次函数图象的性质解题.
解答 解:∵开口向上,
∴a>0,
又∵对称轴为x=$\frac{1}{4}$,
∴-$\frac{b}{2a}$=$\frac{1}{4}$,
∴a=-2b,故③错误;
∵图象与x轴一个交点为($\frac{3}{2}$,0),
∴a+b+c<0,
∴①正确;
∵图象与x轴有两个交点,
∴b2-4ac>0,
即4ac-b2<0,故④正确;
∵对称轴为x=$\frac{1}{4}$,图象与x轴一个交点为($\frac{3}{2}$,0),
∴图象与x轴的另一个交点为(-1,0),
∴当x=-1时,y=0,
∴a-b+c=0,
即a+c=b,故②正确;
所以其中正确的有①②④.
故选B.
点评 本题考查了二次函数y=ax2+bx+c(a≠0)的图象与系数的关系:a>0,开口向上;a<0,开口向下;a与b同号,对称轴在y轴的左侧;a与b异号,对称轴在y轴的右侧;△>0,抛物线与x轴有两个公共点;△<0,抛物线与x轴没有公共点;△=0,抛物线与x轴只有一个公共点.

练习册系列答案
相关题目
8.关于x的方程(a-6)x2-8x+6=0有实数根,下列整数不满足a的取值的是( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
5.下列式子正确的是( )
| A. | ±$\sqrt{9}$=±3 | B. | $\root{3}{-8}$=2 | C. | $\sqrt{{(-3)}^{2}}$=-3 | D. | ±$\sqrt{4}$=2 |
12.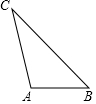 如图,△ABC是一块三角边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
如图,△ABC是一块三角边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
 如图,△ABC是一块三角边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
如图,△ABC是一块三角边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )| A. | 三条高的交点 | B. | 三条中线的交点 | ||
| C. | 三边垂直平分线的交点 | D. | 三个内角角平分线的交点 |
9. 如图,图中有一长、宽、高分别为5cm,4cm,3cm的木箱,在它里面放入一根细木条(木条的粗细,变形忽略不计),要求木条不能露出木箱,请你算一算,能放入的细木条的最大长度是( )
如图,图中有一长、宽、高分别为5cm,4cm,3cm的木箱,在它里面放入一根细木条(木条的粗细,变形忽略不计),要求木条不能露出木箱,请你算一算,能放入的细木条的最大长度是( )
 如图,图中有一长、宽、高分别为5cm,4cm,3cm的木箱,在它里面放入一根细木条(木条的粗细,变形忽略不计),要求木条不能露出木箱,请你算一算,能放入的细木条的最大长度是( )
如图,图中有一长、宽、高分别为5cm,4cm,3cm的木箱,在它里面放入一根细木条(木条的粗细,变形忽略不计),要求木条不能露出木箱,请你算一算,能放入的细木条的最大长度是( )| A. | $\sqrt{41}$cm | B. | $\sqrt{34}$cm | C. | 5$\sqrt{2}$cm | D. | 5$\sqrt{3}$cm |
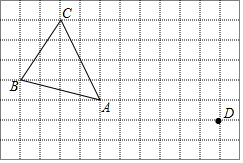 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
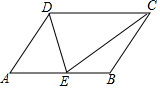 如图,平行四边形ABCD中,E是AB上一点,DE、CE分别是∠ADC、∠BCD的平分线,若AD=5,DE=6,则平行四边形的面积为( )
如图,平行四边形ABCD中,E是AB上一点,DE、CE分别是∠ADC、∠BCD的平分线,若AD=5,DE=6,则平行四边形的面积为( )