题目内容
19. 在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.(1)若∠BAC=50°,则∠AEB=20°;
(2)求证:∠AEB=∠ACF;
(3)若AB=3,则EF2+BF2的值为18.
分析 (1)根据等腰直角三角形的旋转得出∠ABE=∠AEB,求出∠BAE,根据三角形内角和定理求出即可;
(2)根据等腰三角形的性质得出∠BAF=∠CAF,根据SAS推出△BAF≌△CAF,根据全等得出∠ABF=∠ACF,即可得出答案;
(3)根据全等得出BF=CF,求出∠CFG=∠EAG=90°,根据勾股定理求出EF2+BF2=EF2+CF2=EC2,EC2=AC2+AE2=2AC2,即可得出答案.
解答 (1)解:∵AB=AC,△ACE是等腰直角三角形,
∴AB=AE,
∴∠ABE=∠AEB,
又∵∠BAC=50°,∠EAC=90°,
∴∠BAE=50°+90°=140°,
∴∠AEB=(180°-140°)÷2=20°;
(2)证明:∵AB=AC,D是BC的中点,
∴∠BAF=∠CAF.
在△BAF和△CAF中,$\left\{\begin{array}{l}AB=AC\\∠BAF=∠CAF,AF=AF\end{array}$,
∴△BAF≌△CAF(SAS).
∴∠ABF=∠ACF.
又∵AB=AC,
∴∠ABE=∠AEB,
∴∠AEB=∠ACF.
(3)解:
∵△BAF≌△CAF,
∴BF=CF.
∴∠AEB=∠ACF,∠AGE=∠FGC.
∴∠CFG=∠EAG=90°.
∴EF2+BF2=EF2+CF2=EC2.
∵△ACE是等腰直角三角形,
∴∠CAE=90°,AC=AE.
∴EC2=AC2+AE2=2AC2=18.
即EF2+BF2=18.
故答案为:18.
点评 本题考查了勾股定理,全等三角形的性质和判定,等腰直角三角形的应用,能综合运用性质进行推理是解此题的关键,题目比较好,有一定的难度.

练习册系列答案
相关题目
 如图,已知?ABCD和?EBFD,求证:AE=CF.
如图,已知?ABCD和?EBFD,求证:AE=CF.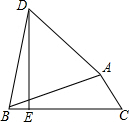 如图,△ABC中,∠C=60°,以AB为边作等边△ABD,过D作DE⊥BC于E.若AC=4,BC=13,则EC=10.5.
如图,△ABC中,∠C=60°,以AB为边作等边△ABD,过D作DE⊥BC于E.若AC=4,BC=13,则EC=10.5.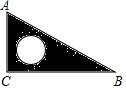 如图,一个直角三角形ABC的直角边BC=a,AC=b,三角形内部圆的半径为r.
如图,一个直角三角形ABC的直角边BC=a,AC=b,三角形内部圆的半径为r.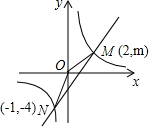 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于M、N两点.
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于M、N两点.