题目内容
4.已知1<x<2,x+$\frac{1}{x-1}$=7.求$\sqrt{x-1}$-$\frac{1}{\sqrt{x-1}}$的值.分析 变形后两边平方,求出(x-1)2+($\frac{1}{x-1}$)2=34,根据完全平方公式求出($\sqrt{x-1}$-$\frac{1}{\sqrt{x-1}}$)2=32,两边开方即可求出答案.
解答 解:∵x+$\frac{1}{x-1}$=7,
∴x-1+$\frac{1}{x-1}$=6.求$\sqrt{x-1}$-$\frac{1}{\sqrt{x-1}}$的值.
∴(x-1+$\frac{1}{x-1}$)2=62,
∴(x-1)2+($\frac{1}{x-1}$)2+2=36,
∴(x-1)2+($\frac{1}{x-1}$)2=34,
∴($\sqrt{x-1}$-$\frac{1}{\sqrt{x-1}}$)2=($\sqrt{x-1}$)2-2+($\frac{1}{\sqrt{x-1}}$)2=34-2=32,
∵1<x<2,
∴$\sqrt{x-1}$<$\frac{1}{\sqrt{x-1}}$,
∴$\sqrt{x-1}$-$\frac{1}{\sqrt{x-1}}$=-$\sqrt{32}$=-4$\sqrt{2}$.
点评 本题考查了二次根式的混合运算和求值,完全平方公式等知识点,能灵活运用公式进行计算是解此题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
2.二次函数y=-3x2+6x变形为y=a(x+m)2+n形式,正确的是( )
| A. | y=-3(x+1)2-3 | B. | y=-3(x-1)2-3 | C. | y=-3(x+1)2+3 | D. | y=-3(x-1)2+3 |
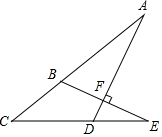 如图,已知EB⊥AD,垂足点为F,若∠C=40°,∠E=25°,则∠A=25°.
如图,已知EB⊥AD,垂足点为F,若∠C=40°,∠E=25°,则∠A=25°. 在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.