题目内容
20．已知a+1＞0，2a-2＜0．（1）求a的取值范围；
（2）若a-b=3，求a+b的取值范围．
分析 （1）解两个不等式组成的方程组即可求得a的范围；
（2）根据a-b=3可得b=a-3，则a+b=2a-3，然后根据a的范围即可求解．
解答 解：（1）根据题意得$\left\{\begin{array}{l}{a+1＞0…①}\\{2a-2＜0…②}\end{array}\right.$，
解①得a＞-1，
解②得a＜1，
则a的范围是-1＜a＜1；
（2）∵a-b=3，
∴b=a-3，
∴a+b=2a-3，
∴--5＜2a-3＜-1，即-5＜a+b＜-1．
点评 本题考查了不等式组的解法以及不等式的性质，把a+b利用a表示是关键．
练习册系列答案
相关题目
10．把点（2，-1）向右平移5个单位得到点（ ）
| A． | （2，-6） | B． | （2，5） | C． | （7，-1） | D． | （-3，-1） |
如图，在△ABC，AC的长为8cm，AC边上的高为BD，当B点在线段BD上向D点运动时，△ABC的面积发生了变化．
15．已知（-1，y1），（1，y2）是直线y=-9x+6上的两个点，则y1，y2的大小关系是（ ）
| A． | y1＞0＞y2 | B． | y1＞y2＞0 | C． | y2＞0＞y1 | D． | 0＞y1＞y2 |
12．若a＜b，则下列各式中一定正确的是（ ）
| A． | a-b＞0 | B． | a+b＞0 | C． | ab＞0 | D． | -a＞-b |
9．在Rt△ABC中，∠C=90°，AB=5，BC=3，则AC为（ ）
| A． | 4 | B． | 16 | C． | $\sqrt{34}$ | D． | 8 |
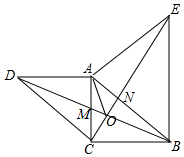已知：如图，△ABC中，∠ACB=90°，AC=BC，以A为直角顶点，分别以AC、AB为一直角边，在△ABC外做等腰直角△ACD和△ABE，连接BD、CE交与点O．