题目内容
15.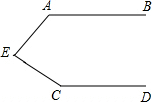 如图,AB∥CD,∠A+∠C+∠AEC=360°.
如图,AB∥CD,∠A+∠C+∠AEC=360°.
分析 过点E作EF∥AB,根据平行线的性质,∠A+∠C+∠AEC就可以转化为两对同旁内角的和.
解答 解:如图,过点E作EF∥AB,
∴∠A+∠AEF=180°;
∵AB∥CD,
∴EF∥CD,
∴∠C+∠FEC=180°,
∴(∠A+∠AEF)+(∠C+∠FEC)=360°,
即∠A+∠C+∠AEC=360°.
故答案为:360.
点评 本题主要考查了平行线的性质,解题时注意:两直线平行时,应该想到它们的性质,由两直线平行的关系得到角之间的数量关系,从而达到解决问题的目的.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
3.-|-125|的立方根是( )
| A. | -$\frac{25}{3}$ | B. | $\frac{25}{3}$ | C. | 5 | D. | -5 |
20. 如图,三角形三个顶点坐标分别为O(0,0),A(2,0),B(1,2).若O,B两点的位置不变,点M在x轴上,则点M在什么位置时,三角形OMB的面积是三角形OAB面积的2倍?(即求出点M的坐标)
如图,三角形三个顶点坐标分别为O(0,0),A(2,0),B(1,2).若O,B两点的位置不变,点M在x轴上,则点M在什么位置时,三角形OMB的面积是三角形OAB面积的2倍?(即求出点M的坐标)
 如图,三角形三个顶点坐标分别为O(0,0),A(2,0),B(1,2).若O,B两点的位置不变,点M在x轴上,则点M在什么位置时,三角形OMB的面积是三角形OAB面积的2倍?(即求出点M的坐标)
如图,三角形三个顶点坐标分别为O(0,0),A(2,0),B(1,2).若O,B两点的位置不变,点M在x轴上,则点M在什么位置时,三角形OMB的面积是三角形OAB面积的2倍?(即求出点M的坐标)
4.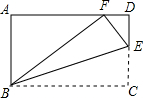 如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )
如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )
 如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )
如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )| A. | 2 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{5}{3}$ |
 如图,∠DAB=∠EAC,AB=AE,AD=AC.求证:DE=BC.
如图,∠DAB=∠EAC,AB=AE,AD=AC.求证:DE=BC.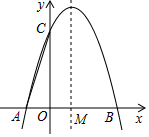 如图,抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于C点,抛物线的对称轴l与x轴交于M点.
如图,抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于C点,抛物线的对称轴l与x轴交于M点.