题目内容
5.先化简,再求值:$\frac{x+2}{x}$÷($\frac{{x}^{2}+4}{{x}^{2}-2x}$-$\frac{4}{x-2}$),其中x=$\sqrt{5}$.分析 根据分式的减法和除法可以化简题目中的式子,然后将x的值代入即可解答本题.
解答 解:$\frac{x+2}{x}$÷($\frac{{x}^{2}+4}{{x}^{2}-2x}$-$\frac{4}{x-2}$)
=$\frac{x+2}{x}÷\frac{{x}^{2}+4-4x}{x(x-2)}$
=$\frac{x+2}{x}•\frac{x(x-2)}{(x-2)^{2}}$
=$\frac{x+2}{x-2}$,
当x=$\sqrt{5}$时,原式=$\frac{\sqrt{5}+2}{\sqrt{5}-2}$=$(\sqrt{5}+2)^{2}=9+4\sqrt{5}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
15.已知四边形ABCD中,对角线AC与BD相交于点O,AD∥BC,下列判断中错误的是( )
| A. | 如果AB=CD,AC=BD,那么四边形ABCD是矩形 | |
| B. | 如果AB∥CD,AC=BD,那么四边形ABCD是矩形 | |
| C. | 如果AD=BC,AC⊥BD,那么四边形ABCD是菱形 | |
| D. | 如果OA=OC,AC⊥BD,那么四边形ABCD是菱形 |
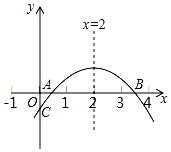 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论: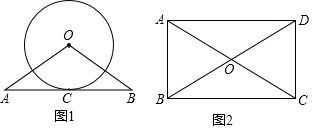
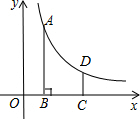 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D.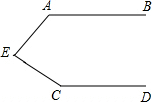 如图,AB∥CD,∠A+∠C+∠AEC=360°.
如图,AB∥CD,∠A+∠C+∠AEC=360°.