题目内容
7.关于x的方程$\frac{2x+m}{x-2}$=1的解是正数,则m的取值范围是m<-2且m≠-4.分析 首先根据$\frac{2x+m}{x-2}$=1,可得x=-m-2;然后根据关于x的方程$\frac{2x+m}{x-2}$=1的解是正数,求出m的取值范围即可.
解答 解:∵$\frac{2x+m}{x-2}$=1,
∴x=-m-2,
∵关于x的方程$\frac{2x+m}{x-2}$=1的解是正数,
∴-m-2>0,
解得m<-2,
又∵x=-m-2≠2,
∴m≠-4,
∴m的取值范围是:m<-2且m≠-4.
故答案为:m<-2且m≠-4.
点评 此题主要考查了分式方程的解,要熟练掌握,解答此题的关键是要明确:在解方程的过程中因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根,增根是令分母等于0的值,不是原分式方程的解.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
17.不等式2x-7<5-2x的正整数解有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
15.分式方程$\frac{x}{x-1}$-2=$\frac{3}{(x-1)(x+2)}$的解是( )
| A. | x=±1 | B. | x=-1+$\sqrt{5}$ | C. | x=2 | D. | x=-1 |
2.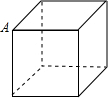 如图,A是正方体小木块(质地均匀)的顶点,将木块随机投掷在水平桌面上,则A与桌面接触的概率是( )
如图,A是正方体小木块(质地均匀)的顶点,将木块随机投掷在水平桌面上,则A与桌面接触的概率是( )
 如图,A是正方体小木块(质地均匀)的顶点,将木块随机投掷在水平桌面上,则A与桌面接触的概率是( )
如图,A是正方体小木块(质地均匀)的顶点,将木块随机投掷在水平桌面上,则A与桌面接触的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
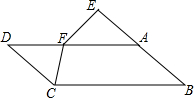 如图:在平行四边形ABCD中,点E在BA的延长线上,且BE=AD,点F在AD上,AF=AB,求证:CF=EF.
如图:在平行四边形ABCD中,点E在BA的延长线上,且BE=AD,点F在AD上,AF=AB,求证:CF=EF. 如图,DE⊥AB于点E,DF⊥AC于点F,DE=DF,AB=AC.求证:BD=CD.
如图,DE⊥AB于点E,DF⊥AC于点F,DE=DF,AB=AC.求证:BD=CD.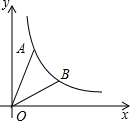 如图,己知点A(1,$\sqrt{3}$)在反比例函数y=$\frac{k}{x}$(x>0)的图象上,连接OA,将线段OA绕点D顺时针方向旋转30°,得到线段OB.
如图,己知点A(1,$\sqrt{3}$)在反比例函数y=$\frac{k}{x}$(x>0)的图象上,连接OA,将线段OA绕点D顺时针方向旋转30°,得到线段OB.