题目内容
19. 如图,DE⊥AB于点E,DF⊥AC于点F,DE=DF,AB=AC.求证:BD=CD.
如图,DE⊥AB于点E,DF⊥AC于点F,DE=DF,AB=AC.求证:BD=CD.
分析 连接AD,由DE⊥AB于点E,DF⊥AC于点F,DE=DF,得出AD是∠EAF的平分线,得出∠1=∠2,由SAS证明△ABD≌△ACD,得出对应边相等即可.
解答 证明:连接AD,如图所示: ∵DE⊥AB于点E,DF⊥AC于点F,DE=DF,
∵DE⊥AB于点E,DF⊥AC于点F,DE=DF,
∴AD是∠EAF的平分线,
∴∠1=∠2,
在△ABD和△ACD中,$\left\{\begin{array}{l}{AB=AC}&{\;}\\{∠1=∠2}&{\;}\\{AD=AD}&{\;}\end{array}\right.$,
∴△ABD≌△ACD(SAS),
∴BD=CD.
点评 本题考查了全等三角形的判定与性质、角平分线的判定与性质;熟练掌握全等三角形的判定方法,证出AD是角平分线是解决问题的关键.

练习册系列答案
相关题目
9.下列各运算中,结果正确的是( )
| A. | 2$\sqrt{3}$+3$\sqrt{2}$=5$\sqrt{5}$ | B. | a8÷a2=a4 | C. | (-3a2)3=-27a6 | D. | (a2+b2)2=a4+b4 |
10. 如图,将Rt△ABC(∠B=25°)绕点A顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )
如图,将Rt△ABC(∠B=25°)绕点A顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )
 如图,将Rt△ABC(∠B=25°)绕点A顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )
如图,将Rt△ABC(∠B=25°)绕点A顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )| A. | 65° | B. | 80° | C. | 105° | D. | 115° |
4.已知⊙O的半径为15,弦AB的长为18,点P在弦AB上且OP=13,则AP的长为( )
| A. | 4 | B. | 14 | C. | 4或14 | D. | 6或14 |
9.已知∠A=40°,则它的余角为( )
| A. | 40° | B. | 50° | C. | 130° | D. | 140° |
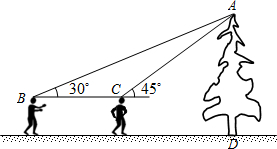 某校初三学生去社会实践,在风景区看到一棵汉白杨树,好高哟,数学老师说请小明和小华同学用数学知识测量,全体同学计算这棵树多高,下面是这两位同学的对话.
某校初三学生去社会实践,在风景区看到一棵汉白杨树,好高哟,数学老师说请小明和小华同学用数学知识测量,全体同学计算这棵树多高,下面是这两位同学的对话.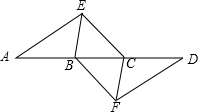 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.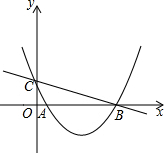 如图,已知抛物线y=ax2-5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.
如图,已知抛物线y=ax2-5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.