题目内容
12.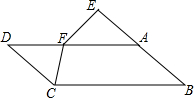 如图:在平行四边形ABCD中,点E在BA的延长线上,且BE=AD,点F在AD上,AF=AB,求证:CF=EF.
如图:在平行四边形ABCD中,点E在BA的延长线上,且BE=AD,点F在AD上,AF=AB,求证:CF=EF.
分析 由四边形ABCD是平行四边形,可得CD∥AB,CD=AB,即可证得∠D=∠EAF,又由BE=AD,AF=AB,易得AE=DF,CD=AF,然后由SAS证得△DCF≌△AFE,即可证得结论.
解答 证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,
∴∠D=∠EAF,
∵BE=AD,AF=AB,
∴AE=DF,CD=AF,
在△CDF和△FAE中,
$\left\{\begin{array}{l}{CD=FA}\\{∠D=∠EAF}\\{DF=AE}\end{array}\right.$,
∴△DCF≌△AFE(SAS),
∴CF=EF.
点评 此题考查了平行四边形的性质以及全等三角形的判定与性质.注意证得△DCF≌△AFE是关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
3.一只盒子中有红球m个,白球6根,黑球n个,每个球除颜色外都相同,从中任取一个球,取得是白球的概率与不是白球的概率相同,那么m与n的关系是( )
| A. | m+n=6 | B. | m+n=3 | C. | m=n=3 | D. | m=2,n=4 |
20.在已知实数-1,0,$\frac{1}{2}$,-$\sqrt{3}$,20150中,最小的一个实数是( )
| A. | -$\sqrt{3}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 0 |
4.已知⊙O的半径为15,弦AB的长为18,点P在弦AB上且OP=13,则AP的长为( )
| A. | 4 | B. | 14 | C. | 4或14 | D. | 6或14 |
1.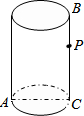 如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点且PC=$\frac{2}{3}$BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点且PC=$\frac{2}{3}$BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
 如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点且PC=$\frac{2}{3}$BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点且PC=$\frac{2}{3}$BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )| A. | (4+$\frac{6}{π}$)cm | B. | 5cm | C. | 2$\sqrt{13}$cm | D. | 7cm |
 中国“蛟龙”号深潜器目前最大测潜极限为7062.68米,某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
中国“蛟龙”号深潜器目前最大测潜极限为7062.68米,某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.