题目内容
14.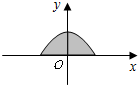 如图所示是二次函数y=-$\frac{1}{2}$x2+2的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为与其最接近的值是( )
如图所示是二次函数y=-$\frac{1}{2}$x2+2的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为与其最接近的值是( )| A. | 4 | B. | $\frac{16}{3}$ | C. | 2π | D. | 8 |
分析 本题不能硬求面积,要观察找一个范围,然后选一个合适的答案.由图形可知阴影部分的面积介于一个三角形和一个半圆之间,问题就好解决了.
解答 解:解:函数y=-$\frac{1}{2}$x2+2与y轴交于(0,2)点,与x轴交于(-2,0)和(2,0)两点,
则三点构成的三角形面积s1=$\frac{1}{2}$×2×4=4,
则以半径为2的半圆的面积为s2=$\frac{1}{2}$π×22=2π,
则阴影部分的面积s有:4<s<2π.
因为选项A、C、D均不在S取值范围内.
故选:B.
点评 此题主要考二次函数的性质,关键是掌握函数图象与x轴相交时,y的值为0.函数图象与y轴相交时,x的值为0.

练习册系列答案
相关题目
4.已知二元一次方程组$\left\{\begin{array}{l}{ax+3y=9}\\{2x-3y=-4}\end{array}\right.$的解,也是二元一次方程6x+y=8的解,求a的值.
5. 如图,AB是⊙O的直径,弦CA=CB,D是AMB上一动点与A、B点不重合),则∠D的度数是( )
如图,AB是⊙O的直径,弦CA=CB,D是AMB上一动点与A、B点不重合),则∠D的度数是( )
 如图,AB是⊙O的直径,弦CA=CB,D是AMB上一动点与A、B点不重合),则∠D的度数是( )
如图,AB是⊙O的直径,弦CA=CB,D是AMB上一动点与A、B点不重合),则∠D的度数是( )| A. | 30° | B. | 40° | C. | 45° | D. | 60° |
9.点M(-1,2)关于x轴对称的点的坐标为( )
| A. | (-1,-2) | B. | (-1,2) | C. | (1,-2) | D. | (2,-1) |
19.已知x=1是一元一次方程2x-a=3的解,则a的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
3.下列各分式中最简分式是( )
| A. | $\frac{{a}^{2}-{b}^{2}}{(a+b)^{2}}$ | B. | $\frac{{b}^{2}-{a}^{2}}{a+b}$ | C. | $\frac{a+b}{a-b}$ | D. | $\frac{20(a-b)}{15(a+b)}$ |
 如图所示,在△ABC中,已知DE∥BC.
如图所示,在△ABC中,已知DE∥BC. 如图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC,求∠DOE的度数.
如图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC,求∠DOE的度数.