题目内容
4. 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )| A. | AD=2OB | B. | CE=EO | C. | ∠OCE=40° | D. | ∠BOC=2∠BAD |
分析 先根据垂径定理得到$\widehat{BC}$=$\widehat{BD}$,CE=DE,再利用圆周角定理得到∠BOC=40°,则根据互余可计算出∠OCE的度数,于是可对各选项进行判断.
解答 解:∵AB⊥CD,
∴$\widehat{BC}$=$\widehat{BD}$,CE=DE,
∴∠BOC=2∠BAD=40°,
∴∠OCE=90°-40°=50°.
故选D.
点评 本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
13.一个三角形的三个内角的度数之比为1:2:3,则这个三角形一定是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰直角三角形 |

 如图,抛物线y1=$\frac{1}{2}$(x+1)2+1与y2=a(x-4)2-3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:
如图,抛物线y1=$\frac{1}{2}$(x+1)2+1与y2=a(x-4)2-3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论: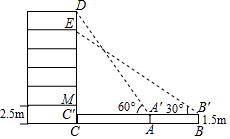 如图,某数学兴趣小组要测量一栋五层居民楼CD的高度.该楼底层为车库,高2.5米;上面五层居住,每层高度相等.测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米.求居民楼的高度(精确到0.1米,参考数据:$\sqrt{3}$≈1.73)
如图,某数学兴趣小组要测量一栋五层居民楼CD的高度.该楼底层为车库,高2.5米;上面五层居住,每层高度相等.测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米.求居民楼的高度(精确到0.1米,参考数据:$\sqrt{3}$≈1.73)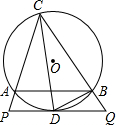 如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.
如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.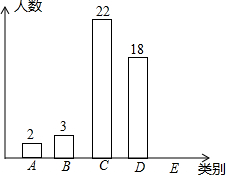 某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间t(单位:小时),将学生分成五类:A类(0≤t≤2),B类(2<t≤4),C类(4<t≤6),D类(6<t≤8),E类(t>8).
某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间t(单位:小时),将学生分成五类:A类(0≤t≤2),B类(2<t≤4),C类(4<t≤6),D类(6<t≤8),E类(t>8).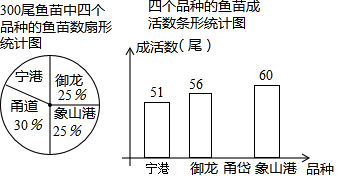
 将一副三角板如图叠放,则图中∠α的度数为15°.
将一副三角板如图叠放,则图中∠α的度数为15°.