题目内容
11.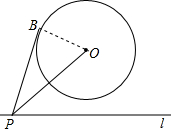 如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点.若PB切⊙O于点B,则PB的最小值是( )
如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点.若PB切⊙O于点B,则PB的最小值是( )| A. | $\sqrt{13}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 2 |
分析 连结OB,如图,根据切线的性质得∠PBO=90°,则利用勾股定理有PB=$\sqrt{O{P}^{2}-O{B}^{2}}$=$\sqrt{O{P}^{2}-{2}^{2}}$,所以当点P运动到点P′的位置时,OP最小时,则PB最小,此时OP=3,然后计算此时的PB即可.
解答 解:连结OB,作OP′⊥l于P′如图, OP′=3,
OP′=3,
∵PB切⊙O于点B,
∴OB⊥PB,
∴∠PBO=90°,
∴PB=$\sqrt{O{P}^{2}-O{B}^{2}}$=$\sqrt{O{P}^{2}-{2}^{2}}$,
当点P运动到点P′的位置时,OP最小时,则PB最小,此时OP=3,
∴PB的最小值为$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$.
故选B.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了垂线段最短.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
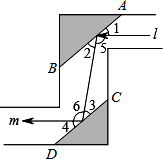 如图是潜望镜工作原理示意图,阴影部分是平行放置在潜望镜里的两面镜子.已知光线经过镜子反射时,有∠1=∠2,∠3=∠4,请解释进入潜望镜的光线l为什么和离开潜望镜的光线m是平行的?
如图是潜望镜工作原理示意图,阴影部分是平行放置在潜望镜里的两面镜子.已知光线经过镜子反射时,有∠1=∠2,∠3=∠4,请解释进入潜望镜的光线l为什么和离开潜望镜的光线m是平行的?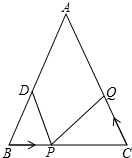 如图,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以3cm/秒的速度由点B向点C运动,同时,点Q在线段CA上由C点向A点运动.
如图,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以3cm/秒的速度由点B向点C运动,同时,点Q在线段CA上由C点向A点运动.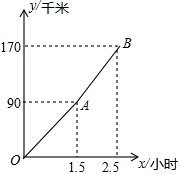 “五一节”期间,小华一家自驾游去了离家170千米的某地,如图是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.下列结论:
“五一节”期间,小华一家自驾游去了离家170千米的某地,如图是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.下列结论: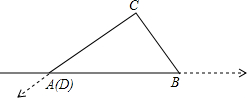 在数轴上点A、B、C、D分别对应数-3、7、13、21,把数轴两次弯折后使点D与点A重合,围成三角形ABC(如图所示),则sin∠ABC的值为$\frac{4}{5}$.
在数轴上点A、B、C、D分别对应数-3、7、13、21,把数轴两次弯折后使点D与点A重合,围成三角形ABC(如图所示),则sin∠ABC的值为$\frac{4}{5}$.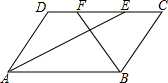 如图,在?ABCD中,AB=8cm,AD=5cm,∠BAD的平分线交CD于点E,∠ABC的平分线交CD于点F,则线段EF的长2cm.
如图,在?ABCD中,AB=8cm,AD=5cm,∠BAD的平分线交CD于点E,∠ABC的平分线交CD于点F,则线段EF的长2cm.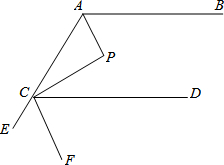 如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.
如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.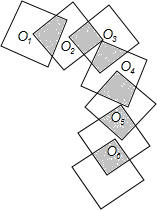 如图,7个正方形的边长均为1,O1、O2、O3、O4、O5、O6是前面六个正方形的中心,同时又是后面六个正方形的顶点,则图中阴影部分的面积是1.5.
如图,7个正方形的边长均为1,O1、O2、O3、O4、O5、O6是前面六个正方形的中心,同时又是后面六个正方形的顶点,则图中阴影部分的面积是1.5.