题目内容
4.超市代销家用电冰箱,从厂家按出厂价2000元进货,然后标价2400元销售,平均每天可售出8台.超市经过调查发现,若每台降价50元,平均每天可多售4台.超市要在销售这种电冰箱中每天利润为4800元,且能让顾客尽可能得到实惠.那超市确定的电冰箱的销售单价是多少?分析 根据升降价问题,表示出每台冰箱的利润=(2400-2000-x)与总的销量(8+$\frac{x}{50}$×4),两者之积,然后解方程求出.
解答 解:设冰箱下降x元,根据题意得:
(2400-2000-x)(8+$\frac{x}{50}$×4)=4800
整理得:x2-300x+20000=0,
解得:x1=100,x2=200
要使顾客得到实惠,取x=200.
定价为:2400-200=2200,
答:冰箱的销售单价定为2200元.
点评 此题考查了一元二次方程的应用,解题的关键是了解利润的求法,难度中等.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
14.已知a是两位数,b是一位数,把b接写在a的后面,就成为一个三位数.这个三位数可表示成( )
| A. | 10a+b | B. | ab | C. | 100a+b | D. | a+10b |
12.下列说法中,正确的是( )
| A. | 方程5x2=x有两个不相等的实数根 | |
| B. | 方程x2-8=0有两个相等的实数根 | |
| C. | 方程2x2-3x+2=0有两个整数根 | |
| D. | 当k>$\frac{2}{3}$时,方程(k-1)x2+2x-3=0有两个不相等的实数根 |
19.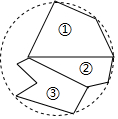 小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
 小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )| A. | ① | B. | ② | C. | ③ | D. | 均不可能 |
9.有下列说法:
①线段的对称轴有两条;
②角是轴对称图形,它的平分线就是它的对称轴;
③到直线a的距离相等的两个点关于直线a对称;
④全等的两个图形成轴对称.
其中正确的有( )
①线段的对称轴有两条;
②角是轴对称图形,它的平分线就是它的对称轴;
③到直线a的距离相等的两个点关于直线a对称;
④全等的两个图形成轴对称.
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16. 如图,把三角形纸片ABC沿DE折叠,当点A落在四边形BCDE外部时,则∠A与∠1、∠2之间的数量关系是( )
如图,把三角形纸片ABC沿DE折叠,当点A落在四边形BCDE外部时,则∠A与∠1、∠2之间的数量关系是( )
 如图,把三角形纸片ABC沿DE折叠,当点A落在四边形BCDE外部时,则∠A与∠1、∠2之间的数量关系是( )
如图,把三角形纸片ABC沿DE折叠,当点A落在四边形BCDE外部时,则∠A与∠1、∠2之间的数量关系是( )| A. | 2∠A=∠1-∠2 | B. | 3∠A=2(∠1-∠2) | C. | 3∠A=2∠1-∠2 | D. | ∠A=∠1-∠2 |
13.有20筐白菜,以每筐30千克为标准,超过或不足的分别用正、负来表示,记录如表:
(1)请将表格补充完整.
(2)20筐白菜中,最重的一筐比最轻的一筐要重多少千克?
(3)求这20筐白菜的总重量.
| 与标准质量的差(单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
| 筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(2)20筐白菜中,最重的一筐比最轻的一筐要重多少千克?
(3)求这20筐白菜的总重量.
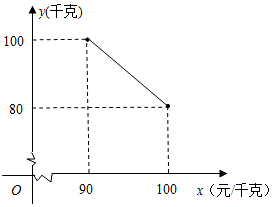 某茶叶专卖店经销一种日照绿茶,每千克成本80元,据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律.
某茶叶专卖店经销一种日照绿茶,每千克成本80元,据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律.