题目内容
17.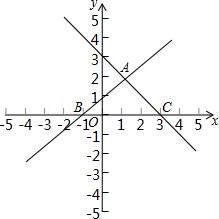 如图,在平面直角坐标系xOy中,直线y=x+1与y=-x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点,在直线AB上存在点E,使得以点E,D,O,A为顶点的四边形是平行四边形,写出$\frac{BE}{CD}$的值.
如图,在平面直角坐标系xOy中,直线y=x+1与y=-x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点,在直线AB上存在点E,使得以点E,D,O,A为顶点的四边形是平行四边形,写出$\frac{BE}{CD}$的值.
分析 分别求得两直线与x轴的交点坐标以及两直线的交点坐标,进而根据待定系数法求得直线OA的解析式,然后分三种情况:①当OE∥AD,ED∥OA时,根据平行线的性质求得直线OE的解析式,进而求得E点的坐标,然后求得直线ED的解析式,然后联立方程求得D的坐标,根据勾股定理分别求得BE和CD的长,从而求得$\frac{BE}{CD}$的值;②当DE∥OA时,OD∥AB时,先求得OD的解析式,进而求得D的坐标,然后根据平行线的性质求得直线DE的解析式,联立方程求得E的坐标,根据勾股定理即可求得BE和CD的长,从而求得$\frac{BE}{CD}$的值;③当AE∥OD时,OE∥AD时,结合①②即可求得BE和CD的长,从而求得$\frac{BE}{CD}$的值.
解答 解:在y=x+1中,当y=0时,x+1=0,
∴x=-1,点B的坐标为(-1,0).
在y=-x+3中,当y=0时,-x+3=0,
∴x=3,点C的坐标为(3,0).
由题意,得$\left\{\begin{array}{l}{y=x+1}\\{y=-x+3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
∴点A的坐标为(1,2).
∴直线OA为y=2x,
①如图①所示:当OE∥AD,ED∥OA时,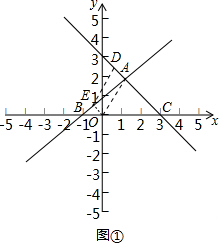
∵OE∥AC,
所以直线OE的解析式为y=-x,
联立OE、AB,得$\left\{\begin{array}{l}{y=x+1}\\{y=-x}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=\frac{1}{2}}\end{array}\right.$,
即E(-$\frac{1}{2}$,$\frac{1}{2}$),
∵ED∥OA,
设直线DE的解析式为y=2x+b,
代入(-$\frac{1}{2}$,$\frac{1}{2}$)得$\frac{1}{2}$=2×(-$\frac{1}{2}$)+b,解得b=$\frac{3}{2}$,
∴直线DE的解析式为y=2x+$\frac{3}{2}$,
联立ED、AC,得$\left\{\begin{array}{l}{y=2x+\frac{3}{2}}\\{y=-x+3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=\frac{5}{2}}\end{array}\right.$,
即D($\frac{1}{2}$,$\frac{5}{2}$),
∴BE=$\sqrt{(-1+\frac{1}{2})^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{2}}{2}$,CD=$\sqrt{(\frac{1}{2}-3)^{2}+(\frac{5}{2})^{2}}$=$\frac{5}{2}$$\sqrt{2}$,
∴$\frac{BE}{CD}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{5\sqrt{2}}{2}}$=$\frac{1}{5}$;
②如图②:当DE∥OA时,OD∥AB时,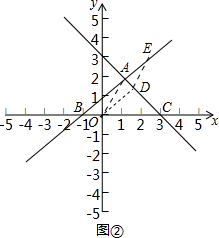
∵OD∥AB,
∴直线OD的解析式为y=x,
联立OD、AC,得$\left\{\begin{array}{l}{y=x}\\{y=-x+3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=\frac{3}{2}}\end{array}\right.$,
D($\frac{3}{2}$,$\frac{3}{2}$).
∵ED∥OA,
设直线DE的解析式为y=2x+b,
代入($\frac{3}{2}$,$\frac{3}{2}$)得,$\frac{3}{2}$=2×($\frac{3}{2}$)+b,解得b=-$\frac{3}{2}$,
∴直线DE的解析式为y=2x-$\frac{3}{2}$,
联立ED、AC,得$\left\{\begin{array}{l}{y=2x-\frac{3}{2}}\\{y=x+1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=\frac{7}{2}}\end{array}\right.$,
即E($\frac{5}{2}$,$\frac{7}{2}$),
∴BE=$\sqrt{(-1-\frac{5}{2})^{2}+(\frac{7}{2})^{2}}$=$\frac{7}{2}$$\sqrt{2}$,CD=$\sqrt{(3-\frac{3}{2})^{2}+(\frac{3}{2})^{2}}$=$\frac{3}{2}$$\sqrt{2}$,
∴$\frac{BE}{CD}$=$\frac{\frac{7\sqrt{2}}{2}}{\frac{3\sqrt{2}}{2}}$=$\frac{7}{3}$;
③如图③,当AE∥OD时,OE∥AD时,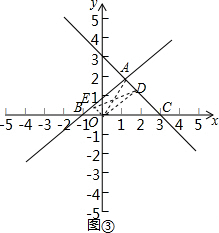
由①②可知E(-$\frac{1}{2}$,$\frac{1}{2}$),D($\frac{3}{2}$,$\frac{3}{2}$),BE=$\frac{\sqrt{2}}{2}$,CD=$\frac{3}{2}$$\sqrt{2}$
∴$\frac{BE}{CD}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{3\sqrt{3}}{2}}$=$\frac{1}{3}$;
综上所述:$\frac{BE}{CD}$的值为$\frac{1}{5}$或$\frac{7}{3}$或$\frac{1}{3}$.
点评 本题主要考查的是一次函数的性质和平行四边形的性质,掌握相互平行的两条直线的一次项系数相同是解题的关系,解答本题主要应用了分类讨论的思想.

问题探究:不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形.所以,当n=3时,m=1
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形,所以,当n=4时,m=0
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形,所以,当n=5时,m=1
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形,所以,当n=6时,m=1
综上所述,可得表①
| n | 3 | 4 | 5 | 6 |
| m | 1 | 0 | 1 | 1 |
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2)分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三
角形?(只需把结果填在表②中)
| n | 7 | 8 | 9 | 10 |
| m |
解决问题:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设n分别等于4k-1、4k、4k+1、4k+2,其中k是整数,把结果填在表 ③中)
| n | 4k-1 | 4k | 4k+1 | 4k+2 |
| m |
其中面积最大的等腰三角形每个腰用了672根木棒.(只填结果)
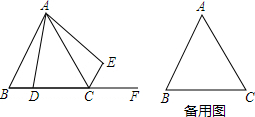
 将一张长方形纸条ABCD按如图所示折叠,若折叠角∠FEC=64°.
将一张长方形纸条ABCD按如图所示折叠,若折叠角∠FEC=64°.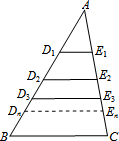 如图,△ABC中,BC=1.若AD1=$\frac{1}{3}$AB,且D1E1∥BC,则D1E1=$\frac{1}{3}$;照这样继续下去,D1D2=$\frac{1}{3}$D1B,且D2E2∥BC;D2D3=$\frac{1}{3}$D2B,且D3E3∥BC;…;Dn-1Dn=$\frac{1}{3}$Dn-1B,且DnEn∥BC,则DnEn=1-($\frac{2}{3}$)n(用含n的式子表示).
如图,△ABC中,BC=1.若AD1=$\frac{1}{3}$AB,且D1E1∥BC,则D1E1=$\frac{1}{3}$;照这样继续下去,D1D2=$\frac{1}{3}$D1B,且D2E2∥BC;D2D3=$\frac{1}{3}$D2B,且D3E3∥BC;…;Dn-1Dn=$\frac{1}{3}$Dn-1B,且DnEn∥BC,则DnEn=1-($\frac{2}{3}$)n(用含n的式子表示).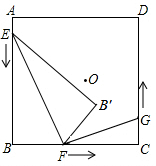 如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm,点E、F、G分别从A、B、C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s.点F的运动速度为3cm/s,点G的运动速度为1.5cm/s.当点F到达点C(即点F与点C重合)时,三个点随之停止运动,在运动过程中,△EBF关于直线EF对称图形是△EB′F,设点E、F、G运动的时间为t(单位:s).
如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm,点E、F、G分别从A、B、C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s.点F的运动速度为3cm/s,点G的运动速度为1.5cm/s.当点F到达点C(即点F与点C重合)时,三个点随之停止运动,在运动过程中,△EBF关于直线EF对称图形是△EB′F,设点E、F、G运动的时间为t(单位:s).