题目内容
5.为了计算1+2+22+23+24+…+29+210的值,我们采用如下的方法:设S=1+2+22+23+24+…+29+210①,则2S=2+22+23+24+…+29+210+211②,由②-①,得S=211-1,利用上述的方法,求1+5+52+53+54+…+52014+52015的值.分析 令S=1+5+52+53+54+…+52014+52015,两边乘以5变形后,相减求出S的值即可.
解答 解:令S=1+5+52+53+54+…+52014+52015,
即5S=5+52+53+54+…+52015+52016,
∴5S-S=52016-1,
则S=$\frac{{5}^{2016}-1}{4}$.
点评 此题考查了有理数的乘方,熟练掌握阅读材料中的方法是解本题的关键.

练习册系列答案
相关题目
13.如图,从边长为(a+3)cm的大正方形纸片中剪去一个边长为(a+1)cm的小正方形(a>0),剩余部分沿虚线剪开,重新拼成一个长方形(不重叠无缝隙),则此长方形的周长为( )
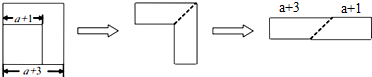

| A. | (4a+12)cm | B. | (4a+8)cm | C. | (2a+6)cm | D. | (2a+4)cm |
10. 如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
 如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )| A. | 180° | B. | 360° | C. | 270° | D. | 540° |
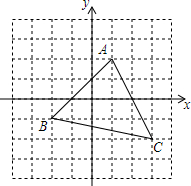 如图,△ABC的三个顶点的坐标分别是A(1,2)、B(-2,-1)、C(3,-2),画出一个与△ABC关于原点对称的△A′B′C′,并分别标出A′、B′、C′的坐标.
如图,△ABC的三个顶点的坐标分别是A(1,2)、B(-2,-1)、C(3,-2),画出一个与△ABC关于原点对称的△A′B′C′,并分别标出A′、B′、C′的坐标.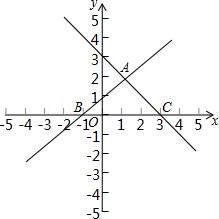 如图,在平面直角坐标系xOy中,直线y=x+1与y=-x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点,在直线AB上存在点E,使得以点E,D,O,A为顶点的四边形是平行四边形,写出$\frac{BE}{CD}$的值.
如图,在平面直角坐标系xOy中,直线y=x+1与y=-x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点,在直线AB上存在点E,使得以点E,D,O,A为顶点的四边形是平行四边形,写出$\frac{BE}{CD}$的值.