题目内容
18.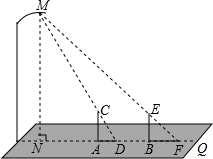 晚饭后,小林和小京在社区广场散步,两人在灯下沿直线NQ移动,如图,当小林正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小京正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小林的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小京身高BE的长.(结果精确到0.01米)
晚饭后,小林和小京在社区广场散步,两人在灯下沿直线NQ移动,如图,当小林正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小京正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小林的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小京身高BE的长.(结果精确到0.01米)
分析 先证明△CAD~△MND,利用相似三角形的性质求得MN=9.6米,再证明△EFB~△MFN,即可解答.
解答 解:由题意得:∠CAD=∠MND=90°,∠CDA=∠MDN,
∴△CAD~△MND,
∴$\frac{CA}{MN}$=$\frac{AD}{ND}$,
∴$\frac{1.6}{MN}$=$\frac{1×0.8}{6×0.8}$,
∴MN=9.6米,
又∵∠EBF=∠MNF=90°,∠EFB=∠MFN,
∴△EFB~△MFN,
∴$\frac{EB}{MN}$=$\frac{BF}{NF}$,
∴$\frac{EB}{9.6}$=$\frac{2×0.8}{11×0.8}$
∴EB≈1.75米.
答:小京身高约为1.75米.
点评 本题考查的是相似三角形的应用,解答此题的关键是利用相似三角形的判定得出△EFB~△MFN.

练习册系列答案
相关题目
6.在平面直角坐标系中,点P(-3,2)关于直线y=x对称点的坐标是( )
| A. | (-3,-2) | B. | (3,2) | C. | (2,-3) | D. | (3,-2) |
13.已知点C是线段AB的黄金分割点(AC>BC),AC=4,则线段AB的长为( )
| A. | 2$\sqrt{5}$-2 | B. | 2$\sqrt{5}$+2 | C. | 6-2$\sqrt{5}$ | D. | 6+2$\sqrt{5}$ |
3.已知:2m+3n=5,则4m•8n=( )
| A. | 16 | B. | 25 | C. | 32 | D. | 64 |
10.某剧院的观众席的座位为扇形,且按下列方式设置:
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
| 排数(x) | 1 | 2 | 3 | 4 | … |
| 座位数(y) | 50 | 53 | 56 | 59 | … |
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
7.今年国庆黄金周,南部山区农家乐共接待15.8万游客,把15.8万用科学记数法表示为( )
| A. | 1.58×105 | B. | 1.58×l04 | C. | 158×103 | D. | 0.158×106 |
 如图,已知一次函数y=kx+b的图象与x轴交于点(3,0),与y轴交于点(0,2),不等式kx+b≥2解集是x≤0.
如图,已知一次函数y=kx+b的图象与x轴交于点(3,0),与y轴交于点(0,2),不等式kx+b≥2解集是x≤0.