题目内容
8.用反证法证明:如果x>$\frac{1}{2}$,那么x2+2x-1≠0.分析 假设x2+2x-1=0,根据一元二次方程的解法解出方程,证明方程的两个根小于$\frac{1}{2}$即可.
解答 解:假设x2+2x-1=0,
x=$\frac{-2±2\sqrt{2}}{2}$,
x1=-1+$\sqrt{2}$,x2=-1-$\sqrt{2}$,
∵2$<\frac{9}{4}$,
∴$\sqrt{2}$$<\frac{3}{2}$,
∴-1+$\sqrt{2}$$<\frac{1}{2}$,
∴x1<$\frac{1}{2}$,
易得x2<$\frac{1}{2}$,
这与已知相矛盾,
∴假设不成立,
∴如果x>$\frac{1}{2}$,那么x2+2x-1≠0.
点评 本题考查的是反证法的应用,反证法的步骤是:假设结论不成立;从假设出发推出矛盾;假设不成立,则结论成立.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
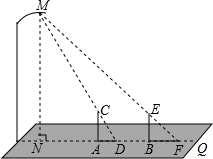 晚饭后,小林和小京在社区广场散步,两人在灯下沿直线NQ移动,如图,当小林正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小京正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小林的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小京身高BE的长.(结果精确到0.01米)
晚饭后,小林和小京在社区广场散步,两人在灯下沿直线NQ移动,如图,当小林正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小京正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小林的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小京身高BE的长.(结果精确到0.01米)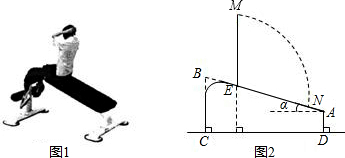
 如图,在四边形ABCD中,AB=3cm,CD=2cm,∠BAD=60°,∠CDA=∠CBA=90°,求四边形ABCD的面积.
如图,在四边形ABCD中,AB=3cm,CD=2cm,∠BAD=60°,∠CDA=∠CBA=90°,求四边形ABCD的面积.