题目内容
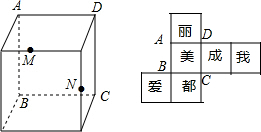
 如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分几何图形的周长为( )
如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分几何图形的周长为( )A、
| ||||
B、4-
| ||||
C、1-
| ||||
| D、4 |
考点:旋转的性质
专题:计算题
分析:B′C′交CD于E,连结AE,如图,根据旋转的性质得AB=AB′=1,∠ABC=∠AB′C′=90°,∠BAB′=30°,再证明Rt△AB′E≌Rt△ADE,得到B′E=DE,所以图中阴影部分几何图形的周长=CE+EB′+AB′+AB+BC=CE+ED+AB′+AB+BC=CD+AB′+AB+BC,即图中阴影部分几何图形的周长为4.
解答:解:B′C′交CD于E,连结AE,如图,
∵正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,
∴AB=AB′=1,∠ABC=∠AB′C′=90°,∠BAB′=30°,
在Rt△AB′E和Rt△ADE中,
,
∴Rt△AB′E≌Rt△ADE(HL),
∴B′E=DE,
∴图中阴影部分几何图形的周长=CE+EB′+AB′+AB+BC
=CE+ED+AB′+AB+BC
=CD+AB′+AB+BC
=1+1+11
=4.
故选D.

∵正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,
∴AB=AB′=1,∠ABC=∠AB′C′=90°,∠BAB′=30°,
在Rt△AB′E和Rt△ADE中,
|
∴Rt△AB′E≌Rt△ADE(HL),
∴B′E=DE,
∴图中阴影部分几何图形的周长=CE+EB′+AB′+AB+BC
=CE+ED+AB′+AB+BC
=CD+AB′+AB+BC
=1+1+11
=4.
故选D.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知△ACD与△BCE,AD与BE相交于P点,若AC=BC,AD=BE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为( )
如图,已知△ACD与△BCE,AD与BE相交于P点,若AC=BC,AD=BE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为( )| A、110° | B、125° |
| C、130° | D、155° |
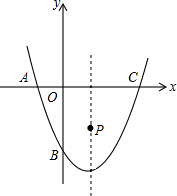 如图,抛物线y=x2-2x-3与x轴交于A,C两点,与y轴交与点B,点P是抛物线对称轴上的一个动点,若使△ABP的周长最小,则点P的坐标为
如图,抛物线y=x2-2x-3与x轴交于A,C两点,与y轴交与点B,点P是抛物线对称轴上的一个动点,若使△ABP的周长最小,则点P的坐标为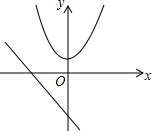 如图,坐标系中有抛物线c:y=x2+m和直线l:y=-2x-2.
如图,坐标系中有抛物线c:y=x2+m和直线l:y=-2x-2.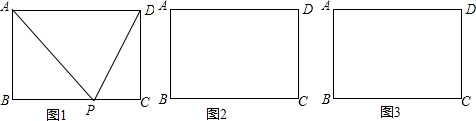
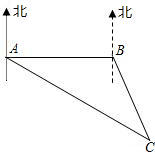 某客轮在C点失事后,海上搜救中心立即通知位于A、B两处的专业救助轮前往出事地点协助搜索.B在A的正东方向,且相距100海里,接到通知后,测得出事地点C在A的南偏东60°,C在B的南偏东30°.B处救助轮赶到出事地点C需要4小时,如果A,B两处救助轮航行速度相同,试问A处救助轮赶到出事地点C需要多长时间?
某客轮在C点失事后,海上搜救中心立即通知位于A、B两处的专业救助轮前往出事地点协助搜索.B在A的正东方向,且相距100海里,接到通知后,测得出事地点C在A的南偏东60°,C在B的南偏东30°.B处救助轮赶到出事地点C需要4小时,如果A,B两处救助轮航行速度相同,试问A处救助轮赶到出事地点C需要多长时间?