题目内容
如图，在Rt△ABC中，∠ACB=90°，AB=10，cosB=| 4 |
| 5 |
考点：解直角三角形
专题：
分析：先在Rt△ABC中，由余弦函数的定义得出cosB=
=
，于是BC=
AB=8．然后在Rt△BCD中，由余弦函数的定义得出cosB=
=
，那么BD=
BC=
，再利用勾股定理得到CD=
=
．
| BC |
| AB |
| 4 |
| 5 |
| 4 |
| 5 |
| BD |
| BC |
| 4 |
| 5 |
| 4 |
| 5 |
| 32 |
| 5 |
| BC2-BD2 |
| 24 |
| 5 |
解答：解：∵在Rt△ABC中，∠ACB=90°，AB=10，cosB=
=
，
∴BC=
AB=8．
∵在Rt△BCD中，cosB=
=
，
∴BD=
BC=
，
∴CD=
=
．
| BC |
| AB |
| 4 |
| 5 |
∴BC=
| 4 |
| 5 |
∵在Rt△BCD中，cosB=
| BD |
| BC |
| 4 |
| 5 |
∴BD=
| 4 |
| 5 |
| 32 |
| 5 |
∴CD=
| BC2-BD2 |
| 24 |
| 5 |
点评：本题考查了解直角三角形，锐角三角函数的定义，勾股定理，求出BC的长是解题的关键．
练习册系列答案
相关题目
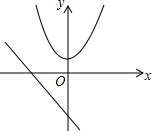如图，坐标系中有抛物线c：y=x2+m和直线l：y=-2x-2．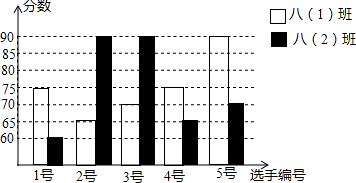
如图，∠C=90°，以AC为半径的圆C与AB相交于点D．若AC=3，CB=4，求BD长．如图所示，其中是轴对称图形的是（ ）
A、 |
B、 |
C、 |
D、 |
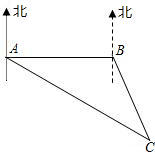某客轮在C点失事后，海上搜救中心立即通知位于A、B两处的专业救助轮前往出事地点协助搜索．B在A的正东方向，且相距100海里，接到通知后，测得出事地点C在A的南偏东60°，C在B的南偏东30°．B处救助轮赶到出事地点C需要4小时，如果A，B两处救助轮航行速度相同，试问A处救助轮赶到出事地点C需要多长时间？
用长为8米的铝合金制成如图所示的窗框，若设窗框的宽为x米，窗户的透光面积为S平方米，则S关于x的函数关系式为