题目内容
14.某地组织20辆汽车装运A,B,C三种苹果42吨到外地销售.按规定每辆车只装一种苹果,且必须装满,每种苹果不少于2车.| 苹果品种 | A | B | C |
| 每辆汽车(吨) | 2.2 | 2.1 | 2 |
| 每吨苹果获利(百元) | 6 | 8 | 5 |
(2)设此次外销活动的利润为W(百元),求W与x之间的函数关系式,x为何值时W(百元)取得最大利润,并安排此时相应的车辆调配方案.
分析 (1)根据有20辆汽车装运A、B、C三种水果,可以表示出有20-x-y辆车装运C种水果,从而得出答案,
(2)从而根据水果总吨数为42,再根据(1)中运费与车辆数即可表示出w,最后由一次函数的性质即可求最大利润以及此时相应的车辆调配方案.
解答 解:(1)由题意得:
2.2x+2.1y+2(20-x-y)=42,
化简得:y=20-2x,
∵$\left\{\begin{array}{l}{x≥2}\\{20-2x≥2}\end{array}\right.$,
∴x的取值范围是:2≤x≤9.
(2)由题意得:
W=6×2.2x+8×2.1(-2x+20)+5×2(20-x-y),
=-10.4x+336,
∵k=-10.4<0,且2≤x≤9,
∴当x=2时,W有最大值,
w最大=-10.4×2+336=315.2(百元),
∴A:2辆;B:16辆;C:2辆.
∴相应的车辆分配方案为:
2辆车装运A种水果,用16辆车装运B种水果,有20-x-y=2辆车装运C种水果.
点评 此题主要考查了一次函数的应用,得出y与x的关系式,以及利用一次函数增减性求最值是解决问题的关键.

练习册系列答案
相关题目
4.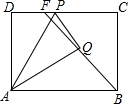 如图,矩形ABCD 中,AB=4,AD=3,P 是边CD 上一点,将△ADP沿直线AP对折,得到△APQ.当射线BQ交线段CD于点F时,DF的最大值是( )
如图,矩形ABCD 中,AB=4,AD=3,P 是边CD 上一点,将△ADP沿直线AP对折,得到△APQ.当射线BQ交线段CD于点F时,DF的最大值是( )
 如图,矩形ABCD 中,AB=4,AD=3,P 是边CD 上一点,将△ADP沿直线AP对折,得到△APQ.当射线BQ交线段CD于点F时,DF的最大值是( )
如图,矩形ABCD 中,AB=4,AD=3,P 是边CD 上一点,将△ADP沿直线AP对折,得到△APQ.当射线BQ交线段CD于点F时,DF的最大值是( )| A. | 3 | B. | 2 | C. | 4-$\sqrt{7}$ | D. | 4-$\sqrt{5}$ |
5.下列计算正确的是( )
| A. | a3•a3=a9 | B. | (a+b)2=a2+b2 | C. | a2÷a2=0 | D. | (a2)3=a6 |
9.温州为了推进“中央绿轴”建设,某园林公司增加了人力进行大型树木移植,现在平均每天比原计划多植树50棵,现在植树600棵所需时间与原计划植树400棵所需时间相同,设原计划平均每天植树x棵,则列出的方程为( )
| A. | $\frac{600}{x+50}$=$\frac{400}{x}$ | B. | $\frac{600}{x}$=$\frac{400}{x-50}$ | C. | $\frac{600}{x-50}$=$\frac{400}{x}$ | D. | $\frac{600}{x}$=$\frac{400}{x+50}$ |
3.郑州已经正式被定为国家中心城市!作为郑州发展的核心,郑州机场2016年全年完成旅客吞吐量2076万次,同比增长20%,将数据2076万用科学记数法表示为( )
| A. | 2.076×108 | B. | 2076×106 | C. | 0.2076×108 | D. | 2.076×107 |
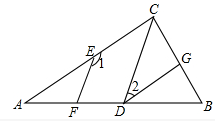 已知:如图,EF∥CD,∠1+∠2=180°.
已知:如图,EF∥CD,∠1+∠2=180°. 位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)