题目内容
4.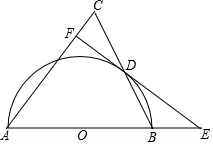 如图,△ABC是等腰三角形,AB=AC,以AB为直径的⊙O与BC交于点D,过点D作⊙O的切线,与AB的延长线交于点E,与AC交于点F.
如图,△ABC是等腰三角形,AB=AC,以AB为直径的⊙O与BC交于点D,过点D作⊙O的切线,与AB的延长线交于点E,与AC交于点F.(1)求证:EF⊥AC;
(2)若⊙O的半径为3,CF=1,求cos∠CAB的值.
分析 (1)连接OD,如图,利用等腰三角形的性质得∠C=∠ABC,∠ODB=∠ABC,则∠ODB=∠C,于是可判断OD∥AC,再根据切线的性质得OD⊥EF,所以EF⊥AC;
(2)先得到AC=AB=6,则AF=5,再证明△EDO∽△EFA,利用相似比得到OE=$\frac{9}{2}$,则AE=$\frac{15}{2}$,然后在Rt△AFE中利用余弦的定义求解.
解答 (1)证明:连接OD,如图,
∵AC=AB,
∴∠C=∠ABC,
∵OD=OB,
∴∠ODB=∠ABC,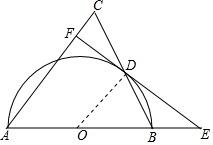
∴∠ODB=∠C,
∴OD∥AC,
∵EF为切线,
∴OD⊥EF,
∴EF⊥AC;
(2)解:∵⊙O的半径为3,
∴AC=AB=6,
∵CF=1,
∴AF=5,
∵OD∥AC,
∴△EDO∽△EFA,
∴$\frac{OD}{AF}$=$\frac{EO}{EA}$,即$\frac{3}{5}$=$\frac{OE}{OE+3}$,
∴OE=$\frac{9}{2}$,
∴AE=3+$\frac{9}{2}$=$\frac{15}{2}$,
在Rt△AFE中,cos∠A=$\frac{AF}{AE}$=$\frac{5}{\frac{15}{2}}$=$\frac{2}{3}$,
即cos∠CAB的值为$\frac{2}{3}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了等腰三角形的性质、相似三角形的判定与性质和锐角三角函数的定义.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14. 已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>0;④4a-2b+c>0.其中正确结论的个数是( )
已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>0;④4a-2b+c>0.其中正确结论的个数是( )
 已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>0;④4a-2b+c>0.其中正确结论的个数是( )
已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>0;④4a-2b+c>0.其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.已知一次函数y=kx+b的图象与直线y=5x+1平行,且过点(2,1),那么此一次函数的解析式为( )
| A. | y=-5x-2 | B. | y=-5x-6 | C. | y=-5x+10 | D. | y=-5x+11 |
12.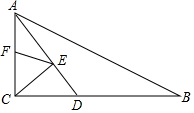 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )| A. | $\frac{40}{3}$ | B. | $\frac{15}{4}$ | C. | $\frac{24}{5}$ | D. | 6 |
19.一组数据2,3,5,4,4,6的中位数和平均数分别是( )
| A. | 4和4 | B. | 4.5和4 | C. | 4和4.8 | D. | 5和4 |
9.温州为了推进“中央绿轴”建设,某园林公司增加了人力进行大型树木移植,现在平均每天比原计划多植树50棵,现在植树600棵所需时间与原计划植树400棵所需时间相同,设原计划平均每天植树x棵,则列出的方程为( )
| A. | $\frac{600}{x+50}$=$\frac{400}{x}$ | B. | $\frac{600}{x}$=$\frac{400}{x-50}$ | C. | $\frac{600}{x-50}$=$\frac{400}{x}$ | D. | $\frac{600}{x}$=$\frac{400}{x+50}$ |
13.为了了解某校七年级学生的视力,从中抽取60名学生进行视力检查,在这次调查中,总体是( )
| A. | 每名学生的视力 | B. | 60名学生的视力 | ||
| C. | 60名学生 | D. | 该校七年级学生的视力 |
 如图,边长为4的正方形ABCD外切于⊙O,切点分别为E、F、G、H.则图中阴影部分的面积为2π+4.
如图,边长为4的正方形ABCD外切于⊙O,切点分别为E、F、G、H.则图中阴影部分的面积为2π+4.