题目内容
20.已知m是一个正整数,记F(x)=|x-m|-(x-m)的值,例如,F(10)=|10-m|-(10-m).若F(1)+F(2)+…+F(20)=30,则m=6.分析 根据F(x)的意义,用含m和绝对值的式子表示出方程F(1)+F(2)+…+F(20)=30,根据m是正整数,可以依次试验,确定m的值.
解答 解:由题意可知:F(1)+F(2)+…+F(30)=30,
∴|1-m|-(1-m)+|2-m|-(2-m)+…+|20-m|-(20-m)=30,
∴|1-m|+|2-m|+|3-m|+…+|20-m|=(1-m)+(2-m)+(3-m)+…+(20-m)+30,
即|1-m|+|2-m|+|3-m|+…+|20-m|=(1+2+3+…+20)-20m+30,
由于m是一个正整数,当m=1时
2-m+3-m+…+20-m=(1+2+3+…+20)-20m+30
(2+3+4+…+20)-19m=1+(2+3+…+20)-19m-m+30
此时m=31,这与m=1矛盾.
当m=2时
m-1+2-m+3-m+…+20-m=(1+2+3+…+20)-20m+30
(-1+2+3+4+…+20)-18m=1+(2+3+…+20)-18m-2m+30
此时m=小数,这与m=正整数矛盾.
当m=3时
m-1+m-2+3-m+…+20-m=(1+2+3+…+20)-20m+30
(-1-2+3+4+…+20)-16m=1+2+(3+4+…+20)-16m-4m+30
此时m=9,这与m=3矛盾.
…
当m=6时
m-1+m-2+m-3+m-4+m-5+6-m+7-m+…+20-m=(1+2+3+…+20)-20m+30
-15+(6+7+…+20)-10m=15+(6+7+…+20)-10m-10m+30
此时m=6,这与m=6相一致.
当m=7时
m-1+m-2+m-3+m-4+m-5+m-6+7-m+…+20-m=(1+2+3+…+20)-20m+30
-21+(7+…+20)-9m=21+(7+…+20)-9m-11m+30
此时m=小数,这与m=7矛盾.
…
当m=20时
m-1+m-2+m-3+m+…+m-20≠(1+2+3+…+20)-20m+30
综上m=6.
故答案为:6
点评 本题考查了绝对值和新定义运算.明白新定义并会运用新定义是解决本题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案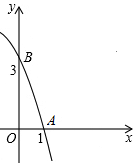 在平面直角坐标系xOy中,开口向下的抛物线y=ax2+bx+c的一部分图象如图所示,它与x轴交于A(1,0),与y轴交于点B (0,3),则a的取值范围是( )
在平面直角坐标系xOy中,开口向下的抛物线y=ax2+bx+c的一部分图象如图所示,它与x轴交于A(1,0),与y轴交于点B (0,3),则a的取值范围是( )| A. | a<0 | B. | -3<a<0 | C. | a<$-\frac{3}{2}$ | D. | $-\frac{9}{2}$<a<$-\frac{3}{2}$ |
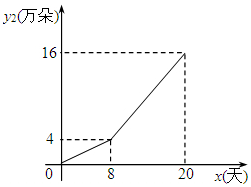 某鲜花销售部在春节前20天内销售一批鲜花.其中,该销售部公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)关系为二次函数,部分对应值如表所示.
某鲜花销售部在春节前20天内销售一批鲜花.其中,该销售部公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)关系为二次函数,部分对应值如表所示.| 时间x(天) | 0 | 4 | 8 | 12 | 16 | 20 |
| 销量y1(万朵) | 0 | 16 | 24 | 24 | 16 | 0 |
(1)求y1与x的二次函数关系式及自变量x的取值范围;
(2)求y2与x的函数关系式及自变量x的取值范围;
(3)当8≤x≤20时,设该花木公司鲜花日销售总量为y万朵,写出y与时间x的函数关系式,并判断第几天日销售总量y最大,并求出此时的最大值.
| A. | 4 | B. | -4 | C. | 8 | D. | -8 |
 如图,已知△ABE≌△ACD,下列选项中不能被证明的等式是( )
如图,已知△ABE≌△ACD,下列选项中不能被证明的等式是( )| A. | AD=AE | B. | DB=AE | C. | DF=EF | D. | DB=EC |

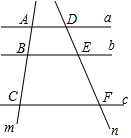 如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.
如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.