题目内容
5.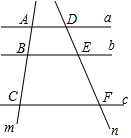 如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.
如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.(1)若AB=3,BC=5,DE=4,求EF的长;
(2)若AB:BC=2:5,DF=10,求EF的长.
分析 (1)根据平行线分线段成比例定理得到$\frac{3}{5}=\frac{4}{EF}$,然后利用比例性质求EF;
(2)根据平行线分线段成比例定理得到$\frac{DE+EF}{EF}=\frac{2+5}{5}$,然后利用比例性质求EF即可.
解答 解:(1)∵a∥b∥c,
∴$\frac{AB}{BC}=\frac{DE}{EF}$,即$\frac{3}{5}=\frac{4}{EF}$,
解得$EF=\frac{20}{3}$;
(2)∵a∥b∥c,
∴$\frac{AB}{BC}=\frac{DE}{EF}=\frac{2}{5}$,
∴$\frac{DE+EF}{EF}=\frac{2+5}{5}$,
解得$EF=\frac{50}{7}$.
点评 本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
16.方程$\frac{x}{4}$=-$\frac{1}{2}$x+3的解为( )
| A. | x=4 | B. | x=$\frac{9}{4}$ | C. | x=-4 | D. | x=$\frac{3}{2}$ |
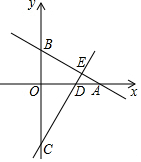 如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+3与x轴、y轴交于点A、B.直线CD与y轴交于点C(0,-6),与x轴相交于点D,与直线AB相交于点E.若△AOB≌△COD,则点E的坐标为($\frac{18}{5}$,$\frac{6}{5}$).
如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+3与x轴、y轴交于点A、B.直线CD与y轴交于点C(0,-6),与x轴相交于点D,与直线AB相交于点E.若△AOB≌△COD,则点E的坐标为($\frac{18}{5}$,$\frac{6}{5}$). 如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=$\frac{10}{3}$或10s时,△POQ是等腰三角形.
如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=$\frac{10}{3}$或10s时,△POQ是等腰三角形.