题目内容
10．
如图，已知△ABE≌△ACD，下列选项中不能被证明的等式是（ ）| A． | AD=AE | B． | DB=AE | C． | DF=EF | D． | DB=EC |
分析 根据全等三角形的性质可得到AD=AE、AB=AC，则可得到BD=CE，∠B=∠C，则可证明△BDF≌△CEF，可得DF=EF，可求得答案．
解答 解：
∵△ABE≌△ACD，
∴AB=AC，AD=AE，∠B=∠C，故A正确；
∴AB-AD=AC-AE，即BD=EC，故D正确；
在△BDF和△CEF中
$\left\{\begin{array}{l}{∠B=∠C}\\{∠BFD=∠CFE}\\{BD=CE}\end{array}\right.$
∴△BDF≌△CEF（ASA），
∴DF=EF，故C正确；
故选B．
点评 本题主要考查全等三角开的性质，掌握全等三角形的对应边相等、对应角相等是解题的关键．
练习册系列答案
相关题目
18．直角三角形的两直角边长分别为3cm、4cm以直角顶点为圆心，2.4cm长为半径的圆与斜边的位置关系是（ ）
| A． | 相交 | B． | 相切 | C． | 相离 | D． | 无法确定 |
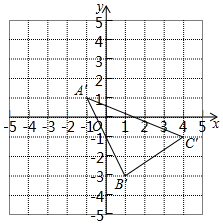在平面直角坐标系中，A，B，C三点的坐标分别为（-5，4），（-3，0），（0，2）．
如图，∠BOC=60°，点A是BO延长线上的一点，OA=10cm，动点P从点A出发沿AB以2cm/s的速度移动，动点Q从点O出发沿OC以1cm/s的速度移动，如果点P、Q同时出发，用t（s）表示移动的时间，当t=$\frac{10}{3}$或10s时，△POQ是等腰三角形．