题目内容
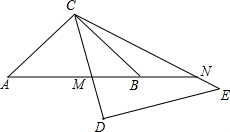 如图,等腰直角三角形ABC,AC=BC,若∠DCE=45°,且CD交AB于点M,CE交AB的延长线于点N,记AM=x,MN=y,BN=z,问以x,y,z为边长的三角形是怎样的三角形?并说明理由.
如图,等腰直角三角形ABC,AC=BC,若∠DCE=45°,且CD交AB于点M,CE交AB的延长线于点N,记AM=x,MN=y,BN=z,问以x,y,z为边长的三角形是怎样的三角形?并说明理由.考点:全等三角形的判定与性质,等腰直角三角形,旋转的性质
专题:
分析:把△BCN绕点C顺时针旋转90°得到△ACN′,连接MN′,根据旋转的性质可得AN′=BN,CN=CN′,∠NCN′=90°,再求出∠MCN′=45°,从而得到∠MCN′=∠DCE,然后利用“边角边”证明△MCN′和△MCN全等,根据全等三角形对应边相等可得MN=MN′,再求出∠MAN′=90°,然后利用勾股定理列式即可.
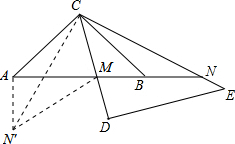
解答:解:如图,把△BCN绕点C顺时针旋转90°得到△ACN′,连接MN′,
由旋转的性质得,AN′=BN,CN=CN′,∠NCN′=90°,
∵∠DCE=45°,
∴∠MCN′=90°-45°=45°,
∴∠MCN′=∠DCE,
在△MCN′和△MCN中,
,
∴△MCN′≌△MCN(SAS),
∴MN=MN′,
∵等腰直角△ABC中,AC=BC,
∴∠BAC=∠ABC=45°,
∴∠CBN=180°-45°=135°,
∴∠MAN′=135°-45°=90°,
∴△AMN′是直角三角形,
∴AM2+AN′2=MN′2,
∴AM2+BN2=MN2,
即x2+z2=y2,
故以x,y,z为边长的三角形是直角三角形.
由旋转的性质得,AN′=BN,CN=CN′,∠NCN′=90°,
∵∠DCE=45°,
∴∠MCN′=90°-45°=45°,
∴∠MCN′=∠DCE,
在△MCN′和△MCN中,
|

∴△MCN′≌△MCN(SAS),
∴MN=MN′,
∵等腰直角△ABC中,AC=BC,
∴∠BAC=∠ABC=45°,
∴∠CBN=180°-45°=135°,
∴∠MAN′=135°-45°=90°,
∴△AMN′是直角三角形,
∴AM2+AN′2=MN′2,
∴AM2+BN2=MN2,
即x2+z2=y2,
故以x,y,z为边长的三角形是直角三角形.
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的性质,旋转的性质,勾股定理和勾股定理逆定理,利用旋转作辅助线构造成全等三角形和直角三角形是解题的关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
若一个数的相反数是2,则这个数是( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
 如图,已知E为直线AD上一点,∠1=∠2,∠B=∠C,请写出图中一组相等的线段
如图,已知E为直线AD上一点,∠1=∠2,∠B=∠C,请写出图中一组相等的线段 如图所示,在长30m,宽20m的花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)
如图所示,在长30m,宽20m的花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)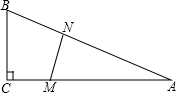 如图,在△ABC中,∠C=90°,BC=5米,AB=10米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
如图,在△ABC中,∠C=90°,BC=5米,AB=10米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.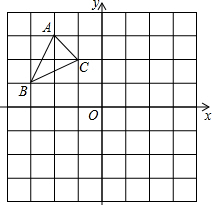 △ABC在如图的平面直角坐标系中,
△ABC在如图的平面直角坐标系中,