Question

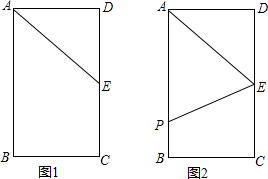
14．如图1，矩形ABCD中，AB=6cm，BC=4cm，E为CD中点．点P从A点出发，沿A-B-C的方向在矩形边上匀速运动，速度为1cm/s，运动到C点停止．设点P运动的时间为t s．（图2为备用图）
（1）当P在AB上，t为何值时，△APE的面积是矩形ABCD面积的$\frac{1}{3}$？
（2）在整个运动过程中，t为何值时，△APE为等腰三角形？

Answer 1

分析 （1）设t秒后，△APE的面积为长方形面积的$\frac{1}{3}$，根据题意得：△APE的面积=$\frac{1}{2}$AP•AD=$\frac{1}{2}$t×4，从而求得t值；
（2）第一种情况，当P在AE垂直平分线上时，AP=EP；第二种情况，P运动到点B上时APE为等腰三角形，此时AE=EP，t=6；第三种情况，P在AB上，AP=PE；解答即可．

解答 解：（1）设t秒后，△APE的面积为长方形面积的$\frac{1}{3}$，
根据题意得：AP=t，
∴△APE的面积=$\frac{1}{2}$AP•AD=$\frac{1}{2}$t×4=$\frac{4×6}{3}$，
解得：t=4，
∴4秒后，△APE的面积为长方形面积的$\frac{1}{3}$；

（2）①当P在AE垂直平分线上时，AP=EP，
过P作PQ⊥AE于Q，∵AD=4，DE=3，
∴AE=5，
∴AQ=2.5，
由△AQP∽△EDA，得：$\frac{AP}{AE}=\frac{AP}{5}$，
即：$\frac{AP}{5}=\frac{2.5}{3}$，
解得：AP=$\frac{25}{6}$，
∴t=$\frac{25}{6}$；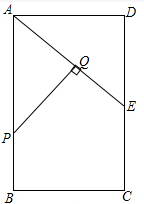
．
②当EA=EB时，AP=6，
∴t=6，
③当AE=AP时，
∴t=5．
∴当t=$\frac{25}{6}$、5、6时，△APE是等腰三角形．

点评 本题考查了四边形的综合知识和动点问题，动点问题更是中考中的热点考题，有一定的难度，解题的关键是能够化动为静，利用等腰三角形的性质求解．