题目内容
8.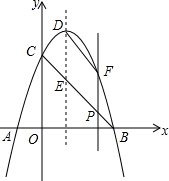 如图,抛物线y=-x2+2x+3与x轴交于点A、点B,与y轴交于点C,其顶点为D.线段BC与抛物线的对称轴交于点E.
如图,抛物线y=-x2+2x+3与x轴交于点A、点B,与y轴交于点C,其顶点为D.线段BC与抛物线的对称轴交于点E.(1)直接写出点B、点C的坐标和抛物线的对称轴;
(2)求线段DE的长度.
分析 (1)令y=0,求出B点坐标,令x=0,求出C点坐标,进而求出抛物线对称轴;
(2)设直线BC的解析式为y=kx+b,求出k和b的值,进而求出E点坐标,即可求出DE的长.
解答 解:(1)令y=-x2+2x+3=0,
解得x=3或x=-1,
即点B的坐标为(3,0),
令x=0,y=3,
即点C的坐标为(0,3),
y=-x2+2x+3=-(x2-2x+1)+4=-(x-1)2+4,
即抛物线的对称轴为x=1;点D坐标为(1,4);
(2)设直线BC的解析式为y=kx+b,
∵点B(3,0),点C(0,3),
∴$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直线BC的解析式为y=-x+3,
当x=1时,y=2,
∴点E(1,2),
∵点D坐标为(1,4);
∴DE=4-2=2.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是求出直线BC的解析式,此题难度不大.

练习册系列答案
相关题目
18.下列四个实数中,最小的是( )
| A. | -$\frac{2}{3}$ | B. | 0 | C. | -3 | D. | 3 |
3.在Rt△ABC中,∠C=90°,sinB=$\frac{12}{13}$,则cosA的值为( )
| A. | $\frac{5}{12}$ | B. | $\frac{12}{5}$ | C. | $\frac{12}{13}$ | D. | $\frac{13}{12}$ |
20.以下叙述中错误的是( )
| A. | $±\sqrt{0.25}$=±0.5 | B. | $±\sqrt{0.25}$=0.5 | C. | 0的平方根是0 | D. | 1是1的平方根 |
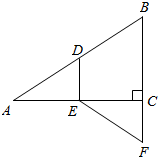 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=$\frac{1}{2}$BC.若AB=12,求EF的长.
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=$\frac{1}{2}$BC.若AB=12,求EF的长.