题目内容
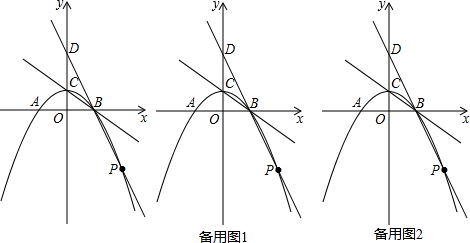
17.若菱形的两条对角线长分别是6和8,则此菱形的周长是20,面积是24.分析 首先根据题意画出图形,然后由菱形的两条对角线长分别是6和8,可求得OA=4,OB=3,再由勾股定理求得边长,继而求得此菱形的周长与面积.
解答  解:如图,菱形ABCD中,AC=8,BD=6,
解:如图,菱形ABCD中,AC=8,BD=6,
∴OA=$\frac{1}{2}$AC=4,OB=$\frac{1}{2}$BD=3,AC⊥BD,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,
∴此菱形的周长是:5×4=20,面积是:$\frac{1}{2}$×6×8=24.
故答案为:20,24.
点评 此题考查了菱形的性质以及勾股定理.注意菱形的面积等于对角线积的一半.

练习册系列答案
相关题目
5.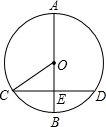 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,若AB=6cm,CD=4cm,则sin∠OCE等于( )
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,若AB=6cm,CD=4cm,则sin∠OCE等于( )
 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,若AB=6cm,CD=4cm,则sin∠OCE等于( )
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,若AB=6cm,CD=4cm,则sin∠OCE等于( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}}{3}$ |
9. 如图所示,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
如图所示,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
 如图所示,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
如图所示,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )| A. | 180° | B. | 270° | C. | 360° | D. | 540° |
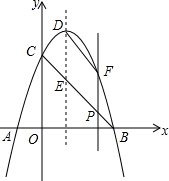 如图,抛物线y=-x2+2x+3与x轴交于点A、点B,与y轴交于点C,其顶点为D.线段BC与抛物线的对称轴交于点E.
如图,抛物线y=-x2+2x+3与x轴交于点A、点B,与y轴交于点C,其顶点为D.线段BC与抛物线的对称轴交于点E. 如图:AB、CD、EF交于O点,AB⊥CD,OG平分∠AOE,∠COE=28°,求∠AOG的度数.
如图:AB、CD、EF交于O点,AB⊥CD,OG平分∠AOE,∠COE=28°,求∠AOG的度数.