题目内容
19.分式方程$\frac{x-3}{{x}^{2}-4}$+$\frac{1}{x-2}$=$\frac{1}{x+2}$的解为x=-1.分析 分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:去分母得:x-3+x+2=x-2,
解得:x=-1,
经检验x=-1是分式方程的解.
故答案为:x=-1
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
10.下列图形中,既是轴对称图形又是中心对称图形的有( )


| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
14.在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个.小颖做摸球实验.她将盒子里面的球搅匀后从中随机摸出一个球记下颜色后放回,不断重复上述过程,多次试验后,得到表中的数据数据,并得出了四个结论,其中正确的是( )
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 70 | 128 | 171 | 302 | 481 | 599 | 1806 |
| 摸到白球的频率$\frac{m}{n}$ | 0.75 | 0.64 | 0.57 | 0.604 | 0.601 | 0.599 | 0.602 |
| A. | 试验1500次摸到白球的频率比试验800次的更接近0.6 | |
| B. | 从该盒子中任意摸出一个小球,摸到白球的概率为0.6 | |
| C. | 当试验次数n为2000时,摸到白球的次数m一定等于1200 | |
| D. | 这个盒子中的白球定有28个 |
9. 如图所示,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
如图所示,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
 如图所示,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
如图所示,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )| A. | 180° | B. | 270° | C. | 360° | D. | 540° |
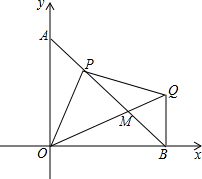 已知:如图,A、B两点坐标为(0,4),B(4,0),P为线段AB上的任一点,过P作OP的垂线与过B点的x轴的垂线交于点Q,OQ与直线AB交于点M.请探究解答下列问题:
已知:如图,A、B两点坐标为(0,4),B(4,0),P为线段AB上的任一点,过P作OP的垂线与过B点的x轴的垂线交于点Q,OQ与直线AB交于点M.请探究解答下列问题: 某城区为了改善全区中、小学办学条件,去年分三批为学校配备了教学器材,其中第三批共投入经费144000元.采购了电子白板16块和投影机8台.已知1块电子白板的单价比1台投影机的多3000元.
某城区为了改善全区中、小学办学条件,去年分三批为学校配备了教学器材,其中第三批共投入经费144000元.采购了电子白板16块和投影机8台.已知1块电子白板的单价比1台投影机的多3000元.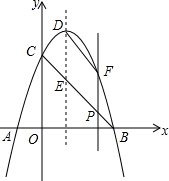 如图,抛物线y=-x2+2x+3与x轴交于点A、点B,与y轴交于点C,其顶点为D.线段BC与抛物线的对称轴交于点E.
如图,抛物线y=-x2+2x+3与x轴交于点A、点B,与y轴交于点C,其顶点为D.线段BC与抛物线的对称轴交于点E.