题目内容
13.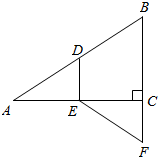 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=$\frac{1}{2}$BC.若AB=12,求EF的长.
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=$\frac{1}{2}$BC.若AB=12,求EF的长.
分析 利用三角形中位线定理以及直角三角形的性质得出DE$\stackrel{∥}{=}$$\frac{1}{2}$BC,DC=$\frac{1}{2}$AB,进而得出四边形DEFC是平行四边形,即可得出答案.
解答  解:连接DC,
解:连接DC,
∵点D,E分别是边AB,AC的中点,
∴DE$\stackrel{∥}{=}$$\frac{1}{2}$BC,DC=$\frac{1}{2}$AB,
∵CF=$\frac{1}{2}$BC,
∴DE$\stackrel{∥}{=}$FC,
∴四边形DEFC是平行四边形,
∴DC=EF,
∴EF=$\frac{1}{2}$AB=6.
点评 此题主要考查了平行四边形的判定与性质以及直角三角形的性质,得出DC=EF是解题关键.

练习册系列答案
相关题目
3. 如图,AB∥CD,∠C=32°,∠E=48°,则∠B的度数为( )
如图,AB∥CD,∠C=32°,∠E=48°,则∠B的度数为( )
 如图,AB∥CD,∠C=32°,∠E=48°,则∠B的度数为( )
如图,AB∥CD,∠C=32°,∠E=48°,则∠B的度数为( )| A. | 120° | B. | 128° | C. | 110° | D. | 100° |
1.中国是一个干旱缺水严重的国家,淡水资源总量约为28000亿立方米,约占全球水资源的6%,将28000用科学记数法表示为( )
| A. | 28×103 | B. | 2.8×104 | C. | 2.8×106 | D. | 0.28×106 |
18.-8的立方根是( )
| A. | ±2 | B. | 2 | C. | -2 | D. | 不存在 |
5.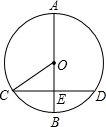 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,若AB=6cm,CD=4cm,则sin∠OCE等于( )
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,若AB=6cm,CD=4cm,则sin∠OCE等于( )
 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,若AB=6cm,CD=4cm,则sin∠OCE等于( )
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,若AB=6cm,CD=4cm,则sin∠OCE等于( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}}{3}$ |
3. 如图,已知AB⊥EF,CD⊥EF,直线AB、EF、GH相交于一点,若∠1=40°,则∠2等于( )
如图,已知AB⊥EF,CD⊥EF,直线AB、EF、GH相交于一点,若∠1=40°,则∠2等于( )
 如图,已知AB⊥EF,CD⊥EF,直线AB、EF、GH相交于一点,若∠1=40°,则∠2等于( )
如图,已知AB⊥EF,CD⊥EF,直线AB、EF、GH相交于一点,若∠1=40°,则∠2等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
 某城区为了改善全区中、小学办学条件,去年分三批为学校配备了教学器材,其中第三批共投入经费144000元.采购了电子白板16块和投影机8台.已知1块电子白板的单价比1台投影机的多3000元.
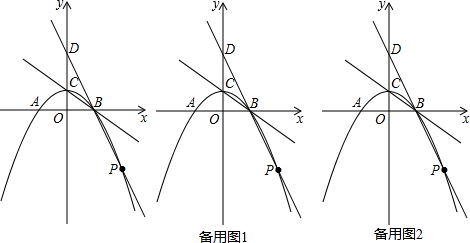
某城区为了改善全区中、小学办学条件,去年分三批为学校配备了教学器材,其中第三批共投入经费144000元.采购了电子白板16块和投影机8台.已知1块电子白板的单价比1台投影机的多3000元.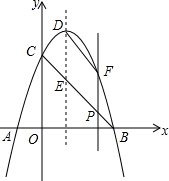 如图,抛物线y=-x2+2x+3与x轴交于点A、点B,与y轴交于点C,其顶点为D.线段BC与抛物线的对称轴交于点E.
如图,抛物线y=-x2+2x+3与x轴交于点A、点B,与y轴交于点C,其顶点为D.线段BC与抛物线的对称轴交于点E.