题目内容
16. 如图,在正方形ABCD中,点E、F分别在AB、BC上,且AE=CF,BE=2AE,点G在DE上,FG⊥DE,垂足是G,若FG=8,则CG=$\frac{27-12\sqrt{10}}{5}$.
如图,在正方形ABCD中,点E、F分别在AB、BC上,且AE=CF,BE=2AE,点G在DE上,FG⊥DE,垂足是G,若FG=8,则CG=$\frac{27-12\sqrt{10}}{5}$.
分析 延长GF交DC的延长线于点M,如图,设正方形ABCD的边长为3a,利用正方形的性质得AE=CF=a,AD=CD=3a,再证明△AED≌△CFM得到AD=CM=3a,则可判断CG为斜边DM上的中线,所以CG=CM,然后根据相似三角形的性质即可得到结论.
解答 解:延长GF交DC的延长线于点M,如图,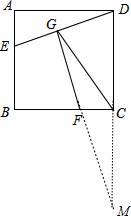 设正方形ABCD的边长为3a,
设正方形ABCD的边长为3a,
∵AE=CF,BE=2AE,
∴AE=CF=a,AD=CD=3a,
∵FD⊥DE,
∴∠EGF=90°,
∴∠GEB+∠BFG=180°,
而∠GEB+∠AED=180°,
∴∠AED=∠BFG,
而∠NFG=∠CFM,
∴∠AED=∠CFM,
在△AED和△CFM中
$\left\{\begin{array}{l}{∠A=∠FCM}\\{AE=CF}\\{∠AED=∠CFM}\end{array}\right.$,
∴△AED≌△CFM,
∴AD=CM=3a,
在Rt△DGM中,∵CD=CM=3a,
∴CG为斜边DM上的中线,
∴CG=CM=3a,
∵∠DGM=∠FCM,∠M=∠M,
∴△CFM∽△GDM,
∴$\frac{FM}{DM}=\frac{CM}{GM}$,
∵FM=$\sqrt{C{F}^{2}+C{M}^{2}}$=$\sqrt{10}$a,
∴$\frac{\sqrt{10}a}{6a}=\frac{3a}{8+\sqrt{10}a}$,
∴a=$\sqrt{10}$,
∴CG=3$\sqrt{10}$.
故答案为:3$\sqrt{10}$.
点评 本题考查了正方形的性质,直角三角形的性质,相似三角形的判定和性质,熟练掌握正方形的性质是解题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
6.一个多边形的内角和是外角和的3倍,它是几边形( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
7.一元二次方程的一般形式是( )
| A. | x2+bx+c=0 | B. | ax2+bx+c=0 | C. | ax2+bx+c=0(a≠0) | D. | 以上答案都不对 |
4.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{36}$ | C. | $\sqrt{\frac{a}{b}}$ | D. | $\sqrt{a+5}$ |
5.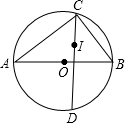 如图,在△ABC中,∠ACB=90°,AB=2,点I是△ABC的内心,CI的延长线交△ABC的外接圆⊙O于点D,则DI的长为( )
如图,在△ABC中,∠ACB=90°,AB=2,点I是△ABC的内心,CI的延长线交△ABC的外接圆⊙O于点D,则DI的长为( )
 如图,在△ABC中,∠ACB=90°,AB=2,点I是△ABC的内心,CI的延长线交△ABC的外接圆⊙O于点D,则DI的长为( )
如图,在△ABC中,∠ACB=90°,AB=2,点I是△ABC的内心,CI的延长线交△ABC的外接圆⊙O于点D,则DI的长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
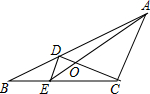 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比=1:4.
如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比=1:4.