Question

11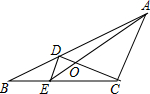．如图，D、E分别是△ABC的边AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S_△DOE：S_△COA=1：25，则S_△BDE与S_△CDE的比=1：4．

Answer 1

分析 根据相似三角形的判定定理得到△DOE∽△COA，根据相似三角形的性质定理得到 $\frac{DE}{AC}$=$\frac{1}{5}$，$\frac{BE}{BC}$=$\frac{DE}{AC}$=$\frac{1}{5}$，结合图形得到$\frac{BE}{EC}$=$\frac{1}{4}$，由此即可得到答案．

解答 解：∵DE∥AC，
∴△DOE∽△COA，又S_△DOE：S_△COA=1：25，
∴$\frac{DE}{AC}$=$\frac{1}{5}$，
∵DE∥AC，
∴$\frac{BE}{BC}$=$\frac{DE}{AC}$=$\frac{1}{5}$，
∴$\frac{BE}{EC}$=$\frac{1}{4}$，
∴S_△BDE与S_△CDE的比是1：4，
故选：B．

点评 本题考查的是相似三角形的判定和性质，掌握相似三角形的面积比等于相似比的平方是解题的关键，属于基础题，中考常考题型．