题目内容
18.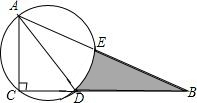 如图,已知△ABC,∠ACB=90°,∠B=30°,AD平分∠BAC,以AD为直径作圆O交AB于E,已知CD=2,则图中阴影部分的面积(用含x的代数式表示)为:2$\sqrt{3}$-$\frac{2}{3}$π.
如图,已知△ABC,∠ACB=90°,∠B=30°,AD平分∠BAC,以AD为直径作圆O交AB于E,已知CD=2,则图中阴影部分的面积(用含x的代数式表示)为:2$\sqrt{3}$-$\frac{2}{3}$π.
分析 根据直角三角形的性质得到∠CAB=60°,AB=4,由角平分线的定义得到∠CAD=∠BAD=30°,求得BC=6,设圆心为O,连接OE,DE,根据圆周角定理得到∠AED=90°,根据直角三角形的性质得到AE=$\frac{1}{2}$AB=2$\sqrt{3}$,根据扇形的面积公式即可得到结论.
解答 解:∵∠ACB=90°,∠B=30°,
∴∠CAB=60°,AB=4,
∵AD平分∠BAC,
∴∠CAD=∠BAD=30°,
∵CD=2,
∴AD=4,AC=2$\sqrt{3}$,
∴BC=6,
∴BD=4,
设圆心为O,连接OE,DE,
∴∠DOE=2∠BAD=60°,
∵AD为直径,
∴∠AED=90°,
∴DE=DC=2,
∵∠B=30°,
∴AE=$\frac{1}{2}$AB=2$\sqrt{3}$,
∵OA=$\frac{1}{2}AD$=2,
∴S扇形ODE=$\frac{60π×{2}^{2}}{360}$=$\frac{2}{3}$π,
∵OA=OD,
∴S△AOE=$\frac{1}{2}$S△ADE=$\frac{1}{2}AE•DE$=$\frac{1}{2}×2\sqrt{3}×2$=2$\sqrt{3}$,
∴S阴影=S△ADB-S扇形-S△AOE=$\frac{1}{2}$×$4×2\sqrt{3}$-$\frac{2}{3}π$-2$\sqrt{3}$=2$\sqrt{3}$-$\frac{2}{3}$π.
故答案为:2$\sqrt{3}$-$\frac{2}{3}$π.
点评 本题考查了扇形的面积的计算,含30°角的直角三角形的性质,圆周角定理,正确的作出辅助线是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
9.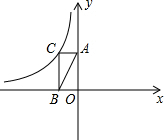 在△ABC中,∠ACB=90°,将Rt△ABC放在如图所示的平面直角坐标系中,△ABC的边AC∥x轴,AC=1,点B在x轴上,点C在函数y=-$\frac{2}{x}$(x<0)的图象上.先将此三角形作关于原点O的对称图形,再向右平移3个单位长度得到△A1B1C1,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,B1C1与此图象交于点P,则点P的纵坐标是( )
在△ABC中,∠ACB=90°,将Rt△ABC放在如图所示的平面直角坐标系中,△ABC的边AC∥x轴,AC=1,点B在x轴上,点C在函数y=-$\frac{2}{x}$(x<0)的图象上.先将此三角形作关于原点O的对称图形,再向右平移3个单位长度得到△A1B1C1,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,B1C1与此图象交于点P,则点P的纵坐标是( )
 在△ABC中,∠ACB=90°,将Rt△ABC放在如图所示的平面直角坐标系中,△ABC的边AC∥x轴,AC=1,点B在x轴上,点C在函数y=-$\frac{2}{x}$(x<0)的图象上.先将此三角形作关于原点O的对称图形,再向右平移3个单位长度得到△A1B1C1,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,B1C1与此图象交于点P,则点P的纵坐标是( )
在△ABC中,∠ACB=90°,将Rt△ABC放在如图所示的平面直角坐标系中,△ABC的边AC∥x轴,AC=1,点B在x轴上,点C在函数y=-$\frac{2}{x}$(x<0)的图象上.先将此三角形作关于原点O的对称图形,再向右平移3个单位长度得到△A1B1C1,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,B1C1与此图象交于点P,则点P的纵坐标是( )| A. | -$\frac{5}{3}$ | B. | -$\frac{3}{4}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
6.在实数-3、0、5、$\sqrt{5}$中,最小的实数是( )
| A. | -3 | B. | 0 | C. | 5 | D. | $\sqrt{5}$ |
13.已知圆O的半径为5,弦AB=8,D为弦AB上一点,且AD=1,过点D作CD⊥AB,交圆O于C,则CD长为( )
| A. | 1 | B. | 7 | C. | 8或1 | D. | 7或1 |
10.解分式方程$\frac{1}{x-1}+\frac{2x}{x+1}=2$时,在方程的两边同时乘以(x-1)(x+1),把原方程化为x+1+2x(x-1)=2(x-1)(x+1),这一变形过程体现的数学思想主要是( )
| A. | 类比思想 | B. | 转化思想 | C. | 方程思想 | D. | 函数思想 |
7. 有一种圆柱体茶叶筒如图所示,则它的俯视图是( )
有一种圆柱体茶叶筒如图所示,则它的俯视图是( )
 有一种圆柱体茶叶筒如图所示,则它的俯视图是( )
有一种圆柱体茶叶筒如图所示,则它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
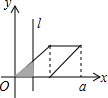
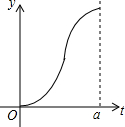 如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆,垂直于x轴的直线l:x=t(0≤t≤a)从原点O向右平行移动,l在移动过程中扫过平面图形的面积为y(图中阴影部分),若y关于t函数的图象大致如图,那么平面图形的形状不可能是
如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆,垂直于x轴的直线l:x=t(0≤t≤a)从原点O向右平行移动,l在移动过程中扫过平面图形的面积为y(图中阴影部分),若y关于t函数的图象大致如图,那么平面图形的形状不可能是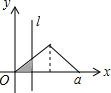

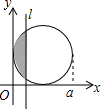
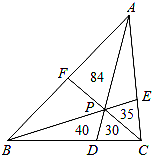 如图,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,则△ABC的面积为( )
如图,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,则△ABC的面积为( )