题目内容
1. 如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,若∠C=50°,求∠BAD的度数.
如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,若∠C=50°,求∠BAD的度数.
分析 首先过点D作DE⊥BC于E,过点D作DF⊥AB交BA的延长线于F,由BD平分∠ABC,根据角平分线的性质,即可得DE=DF,又由AD=CD,即可判定Rt△CDE≌Rt△ADF,则可证得∠A+∠C=180°,即可得到结论.
解答  解:过点D作DE⊥BC于E,过点D作DF⊥AB交BA的延长线于F,
解:过点D作DE⊥BC于E,过点D作DF⊥AB交BA的延长线于F,
∵BD平分∠ABC,
∴DE=DF,∠DEC=∠F=90°,
在RtCDE和Rt△ADF中,
$\left\{\begin{array}{l}{CD=AD}\\{DE=DF}\end{array}\right.$,
∴Rt△CDE≌Rt△ADF(HL),
∴∠FAD=∠C,
∴∠BAD+∠C=∠BAD+∠FAD=180°,
∵∠C=50°,
∴∠BAD=130°.
点评 此题考查了角平分线的性质与全等三角形的判定与性质.此题难度适中,解题的关键是准确作出辅助线,掌握数形结合思想的应用.

练习册系列答案
相关题目
13.若规定收入为“+”,那么支出40元表示( )
| A. | +40元 | B. | -40元 | C. | 0 | D. | +80元 |
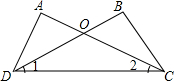 题目:如图,已知AC,BD相交于点0.∠A=∠B,∠1=∠2,试说明△AOD≌△BOC.
题目:如图,已知AC,BD相交于点0.∠A=∠B,∠1=∠2,试说明△AOD≌△BOC.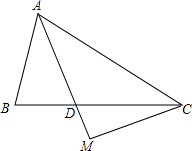 在△ABC中,AD平分∠BAC,且AB=AD,过点C作CM⊥AD交AD延长线于M.
在△ABC中,AD平分∠BAC,且AB=AD,过点C作CM⊥AD交AD延长线于M.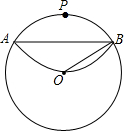 如图,⊙O为一张直径为6的圆形纸片,现将⊙O上任意一点P与圆心O重合折叠,得折痕AB.求折痕AB的长.
如图,⊙O为一张直径为6的圆形纸片,现将⊙O上任意一点P与圆心O重合折叠,得折痕AB.求折痕AB的长. 如图,AB=DC,∠A=∠D,求证:∠B=∠C.
如图,AB=DC,∠A=∠D,求证:∠B=∠C. 如图所示,直线AB和CD相交于点O,∠E0C=90°,∠COA+∠B0D=50°,求∠E0B的度数.
如图所示,直线AB和CD相交于点O,∠E0C=90°,∠COA+∠B0D=50°,求∠E0B的度数.