题目内容
9.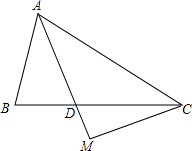 在△ABC中,AD平分∠BAC,且AB=AD,过点C作CM⊥AD交AD延长线于M.
在△ABC中,AD平分∠BAC,且AB=AD,过点C作CM⊥AD交AD延长线于M.(1)若AC=BC,求∠B的度数并探究AB+AC与AM的数量关系,并证明;
(2)若AC≠BC,则(1)中AB+AC与AM的数量关系还会成立吗?请说明理由.
分析 (1)根据等腰三角形的性质得到∠B=∠ADB∠BAC,由AD平分∠BAC,于是得到∠CAD=$\frac{1}{2}$∠BAC=$\frac{1}{2}∠$ADC,求得∠DAC=∠ACD,根据三角形的内角和求得∠B,延长AM至N,使DM=MN,连接CN,求得CD=CN,得出∠ANC=∠ACN,进而求得AC=AN,所以AB+AC=AD+AN=AD+AM+MN=AD+AM+DM=2AM,即可求得结论;
(2)延长AM至N,使DM=MN,连接CN,求得CD=CN,得出∠ANC=∠ACN,进而求得AC=AN,所以AB+AC=AD+AN=AD+AM+MN=AD+AM+DM=2AM,即可求得结论.
解答 解:(1)∵AB=BC,
∴∠B=∠BAC,
∵AB=AD,
∴∠B=∠ADB,
∵AD平分∠BAC,
∴∠CAD=$\frac{1}{2}$∠BAC=$\frac{1}{2}∠$ADC,
∵∠ADC=∠DAC+∠ACD,
∴∠DAC=∠ACD,
∴∠B=∠BAC=2∠ACB,
∵∠B+∠BAC+∠ACB=180°,
∴∠B=∠ACB=72°,
如图1,延长AM至N,使DM=MN,连接CN,
∵CM⊥AD,DM=MN,
∴CN=CD,
∴∠CDN=∠DNC,
∴∠DNC=∠ADB,
∵AD=AB,
∴∠B=∠ADB,
∴∠B=∠ANC,
∵∠BAD=∠CAD,
∴∠ADB=∠ACN,
∴∠ANC=∠ACN,
∴AN=AC,
∴AB+AC=AD+AN=AD+AM+MN=AD+AM+DM=2AM,
∴AM=$\frac{1}{2}$(AB+AC).
(2)AM=$\frac{1}{2}$(AB+AC),
理由:如图2,延长AM至N,使DM=MN,连接CN,
∵CM⊥AD,DM=MN,
∴CN=CD,
∴∠CDN=∠DNC,
∴∠DNC=∠ADB,
∵AD=AB,
∴∠B=∠ADB,
∴∠B=∠ANC,
∵∠BAD=∠CAD,
∴∠ADB=∠ACN,
∴∠ANC=∠ACN,
∴AN=AC,
∴AB+AC=AD+AN=AD+AM+MN=AD+AM+DM=2AM,
∴AM=$\frac{1}{2}$(AB+AC).
点评 本题考查了线段的垂直平方线的性质,等腰三角形的判定和性质,角的平分线的性质;此题利用辅助线构造等腰三角形,得出AN=AC是关键.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案| A. | 若$\frac{x}{a}$=$\frac{y}{a}$,则x=y | B. | 若x2=y2,则-4ax2=-4ay2 | ||
| C. | 若-$\frac{1}{4}$x=-6,则x=$\frac{3}{2}$ | D. | 若1=x,则x=1 |

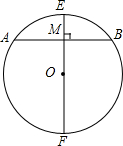 如图所示,M为⊙0内任一不与点O重合的点,连接0M,AB为过M点且与0M垂直的一条弦,EF为过M点的一条直径,求证:在过M点的所有弦中,AB是最短的一条,EF是最长的一条.
如图所示,M为⊙0内任一不与点O重合的点,连接0M,AB为过M点且与0M垂直的一条弦,EF为过M点的一条直径,求证:在过M点的所有弦中,AB是最短的一条,EF是最长的一条. 已知a,b,c在数轴上位置如图,化简:($\sqrt{-a+c}$)2+$\sqrt{(2a+b-c)^{2}}$+$\root{2}{(2b+c)^{2}}$.
已知a,b,c在数轴上位置如图,化简:($\sqrt{-a+c}$)2+$\sqrt{(2a+b-c)^{2}}$+$\root{2}{(2b+c)^{2}}$. 如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,若∠C=50°,求∠BAD的度数.
如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,若∠C=50°,求∠BAD的度数. 如图,若BD、CD分别平分∠ABC和∠ACB,过D作DE∥AB交BC于E,作DF∥AC交BC于F,求证:BC的长等于△DEF的周长.
如图,若BD、CD分别平分∠ABC和∠ACB,过D作DE∥AB交BC于E,作DF∥AC交BC于F,求证:BC的长等于△DEF的周长.