题目内容
6.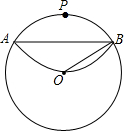 如图,⊙O为一张直径为6的圆形纸片,现将⊙O上任意一点P与圆心O重合折叠,得折痕AB.求折痕AB的长.
如图,⊙O为一张直径为6的圆形纸片,现将⊙O上任意一点P与圆心O重合折叠,得折痕AB.求折痕AB的长.
分析 连接PO,由折叠的性质可知点OP⊥AB,然后根据特殊锐角三角函数值可知∠OAB=30°,然后利用勾股定理和垂径定理求解即可.
解答 解:连接PO交AB于点C,连接OA.
由折叠的性质可知:PO⊥AB,PC=OC=1.5.
∵OC⊥AB,
∴AB=2AC.
在Rt△ACO中,AC=$\sqrt{A{O}^{2}-O{C}^{2}}$=$\sqrt{{3}^{2}-1.{5}^{2}}$=$\frac{3\sqrt{3}}{2}$.
∴AB=3$\sqrt{3}$.
点评 本题主要考查的是翻折的性质、勾股定理、垂径定理的应用,得到△ACO的形状和OA、OC的长度是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
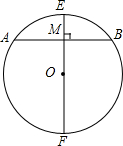 如图所示,M为⊙0内任一不与点O重合的点,连接0M,AB为过M点且与0M垂直的一条弦,EF为过M点的一条直径,求证:在过M点的所有弦中,AB是最短的一条,EF是最长的一条.
如图所示,M为⊙0内任一不与点O重合的点,连接0M,AB为过M点且与0M垂直的一条弦,EF为过M点的一条直径,求证:在过M点的所有弦中,AB是最短的一条,EF是最长的一条. 如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,若∠C=50°,求∠BAD的度数.
如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,若∠C=50°,求∠BAD的度数. 如图,已知AB∥CD,OA=OD,AE=DF.
如图,已知AB∥CD,OA=OD,AE=DF. 如图,已知AB=AC,∠B=∠C,BE与CD相交于点O,求证:△OBD≌△OCE.
如图,已知AB=AC,∠B=∠C,BE与CD相交于点O,求证:△OBD≌△OCE.