题目内容
8. 如图,矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD于E,若∠OAE=24°,则∠BAE的度数是( )
如图,矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD于E,若∠OAE=24°,则∠BAE的度数是( )| A. | 24° | B. | 33° | C. | 42° | D. | 43° |
分析 由直角三角形的性质求出∠AOE=66°,由矩形的性质得出OA=OB,由等腰三角形的性质和三角形内角和定理得出∠OAB=∠OBA=57°,∠BAE=∠OAB-∠OAE,即可得出结果.
解答 解:∵AE⊥BD,
∴∠AEO=90°,
∴∠AOE=90°-∠OAE=66°,
∵四边形ABCD是矩形,
∴OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
∴∠OAB=∠OBA=$\frac{1}{2}$(180°-66°)=57°,
∴∠BAE=∠OAB-∠OAE=33°;
故选:B.
点评 本题考查了矩形的性质、等腰三角形的性质、三角形内角和定理、直角三角形的性质;熟练掌握矩形的性质,由等腰三角形的性质得出∠OAB=57°是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13. 如图,在△ABC中,∠BAC=50°,把△ABC沿EF折叠,C对应点恰好与△ABC的外心O重合,则∠CFE的度数是( )
如图,在△ABC中,∠BAC=50°,把△ABC沿EF折叠,C对应点恰好与△ABC的外心O重合,则∠CFE的度数是( )
 如图,在△ABC中,∠BAC=50°,把△ABC沿EF折叠,C对应点恰好与△ABC的外心O重合,则∠CFE的度数是( )
如图,在△ABC中,∠BAC=50°,把△ABC沿EF折叠,C对应点恰好与△ABC的外心O重合,则∠CFE的度数是( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
 实数a、b、c在数轴上的位置如图所示,试化简:|c-b|+|b-a|-|c|.
实数a、b、c在数轴上的位置如图所示,试化简:|c-b|+|b-a|-|c|.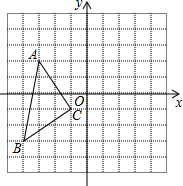 如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴对称的△A1B1C1,并求出△ABC的面积.
如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴对称的△A1B1C1,并求出△ABC的面积. 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,下列结论正确的有( )
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,下列结论正确的有( ) 在边长为1的小正方形网格中,△AOB的顶点均在格点上.
在边长为1的小正方形网格中,△AOB的顶点均在格点上. 已知直线y=x-2t与抛物线y=a(x-t)2+k(a>0,t≥0,a,t,k为已知数),在t=2时,直线刚好经过抛物线的顶点.
已知直线y=x-2t与抛物线y=a(x-t)2+k(a>0,t≥0,a,t,k为已知数),在t=2时,直线刚好经过抛物线的顶点.