题目内容
1.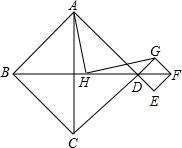 四边形ABCD与四边形DEFG都是正方形,点H为BF的中点,连接HA,HG.若三点B、D、F在同一直线上,如图探索HA与HG的数量及位置关系,并予以证明.
四边形ABCD与四边形DEFG都是正方形,点H为BF的中点,连接HA,HG.若三点B、D、F在同一直线上,如图探索HA与HG的数量及位置关系,并予以证明.
分析 结论:AH=GH,AH⊥HG,欲证明AH=HG,AH⊥GH,只要证明△ANH≌△HOG,根据条件可以得到AN=HO,NH=GO由此即可解决问题.
解答 解:结论AH=HG,AH⊥GH, 理由如下:
理由如下:
连接EG交BF于O,
∵四边形ABCD与四边形DEFG都是正方形,
∴∠ANH=∠HOG=90°,ND=$\frac{1}{2}BD$,DO=$\frac{1}{2}$DF,
∴NO=$\frac{1}{2}$BF,
∵BH=$\frac{1}{2}$BF,
∴BH=NO,
∴BN=HO=AN,
∵BH=BN+NH=BN+OD,
∴NH=DO=GO,
在△ANH和△HOG中,
$\left\{\begin{array}{l}{AN=OH}\\{∠ANH=∠HOG}\\{NH=GO}\end{array}\right.$,
∴△ANH≌△HOG,
∴AH=HG,∴∠AHN=∠HGO,
∵∠GHO+∠HGO=90°,
∴∠AHN+∠GHO=90°,
∴∠AHG=90°,
∴AH⊥HG,
∴AH=HG,AH⊥HG.
点评 本题考查正方形的性质、全等三角形的判定和性质,解题的关键是利用中点定义,结合线段和差定义证明线段相等,属于中考常考题型.

练习册系列答案
相关题目
7.下列函数:①C=2πr;②y=2(3-x);③m=$\frac{2-n}{z}$;④S=x(50-x);⑤t=$\frac{100}{v}$,其中,是一次函数的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.正五边形的中心角等于( )
| A. | 18° | B. | 36° | C. | 54° | D. | 72° |
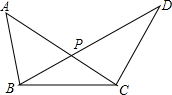 如图,已知△ABC≌△DCB,求证:AP=DP,BP=CP.
如图,已知△ABC≌△DCB,求证:AP=DP,BP=CP. 如图,E,F是四边形ABCD的对角线BD上的两点,AB=CD,AD=CB,DF=BE.求证:AE∥CF.
如图,E,F是四边形ABCD的对角线BD上的两点,AB=CD,AD=CB,DF=BE.求证:AE∥CF.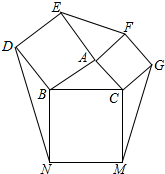 如图,以△ABC的边AB、AC、BC为一边,分别向三角形的外侧作正方形ABDE,正方形ACGF、正方形BCMN
如图,以△ABC的边AB、AC、BC为一边,分别向三角形的外侧作正方形ABDE,正方形ACGF、正方形BCMN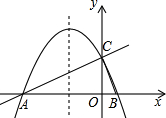 如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A,C两点,与x轴的另一交点为点B.
如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A,C两点,与x轴的另一交点为点B.