题目内容
9.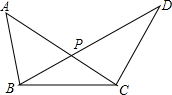 如图,已知△ABC≌△DCB,求证:AP=DP,BP=CP.
如图,已知△ABC≌△DCB,求证:AP=DP,BP=CP.
分析 根据全等三角形的性质得出AB=CD,∠A=∠D,∠ABC=∠DCB,∠DBC=∠ACB,进而利用ASA证明△ABP与△DCP全等即可.
解答 证明:∵△ABC≌△DCB,
∴AB=CD,∠A=∠D,∠ABC=∠DCB,∠DBC=∠ACB,
∴∠ABP=∠DCP,
在△ABP与△DCP中,
$\left\{\begin{array}{l}{∠A=∠D}\\{AB=CD}\\{∠ABP=∠DCP}\end{array}\right.$,
∴△ABP≌△DCP(ASA),
∴AP=DP,BP=CP.
点评 本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
18.如果a表示一个负数,则|a|等于( )
| A. | a | B. | 0 | C. | -a | D. | 不确定 |
 如图,已知△ABC和△ADE是等边三角形,联结BD、CE.
如图,已知△ABC和△ADE是等边三角形,联结BD、CE.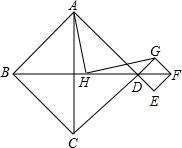 四边形ABCD与四边形DEFG都是正方形,点H为BF的中点,连接HA,HG.若三点B、D、F在同一直线上,如图探索HA与HG的数量及位置关系,并予以证明.
四边形ABCD与四边形DEFG都是正方形,点H为BF的中点,连接HA,HG.若三点B、D、F在同一直线上,如图探索HA与HG的数量及位置关系,并予以证明.