题目内容
18.计算:(1)2$\sqrt{12}$+4$\sqrt{\frac{1}{27}}$-$\sqrt{48}$
(2)(4$\sqrt{6}$-4$\sqrt{\frac{1}{2}}$+3$\sqrt{8}$)÷2$\sqrt{2}$
(3)(7$\sqrt{2}$+2$\sqrt{6}$)(2$\sqrt{6}$-7$\sqrt{2}$)
(4)(6$\sqrt{\frac{x}{4}}$-2x$\sqrt{\frac{1}{x}}$)÷3$\sqrt{x}$.
分析 (1)首先把二次根式进行化简,然后合并同类二次根式即可;
(2)首先对括号内的根式化简,合并,然后进行二次根式的除法运算即可;
(3)利用平方差公式即可求解;
(4)首先对括号内的根式化简,合并,然后进行二次根式的除法运算即可.
解答 解:(1)原式=4$\sqrt{3}$+$\frac{4\sqrt{3}}{9}$-4$\sqrt{3}$=$\frac{4\sqrt{3}}{9}$;
(2)原式=(4$\sqrt{6}$-2$\sqrt{2}$+6$\sqrt{2}$)÷2$\sqrt{2}$=(4$\sqrt{6}$+4$\sqrt{2}$)÷2$\sqrt{2}$=2$\sqrt{3}$+2;
(3)原式=(2$\sqrt{6}$)2-(7$\sqrt{2}$)2=24-98=-74;
(4)原式=(3$\sqrt{x}$-2$\sqrt{x}$)÷3$\sqrt{x}$=$\sqrt{x}$÷3$\sqrt{x}$=$\frac{1}{3}$.
点评 本题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列计算正确的是( )
| A. | 2m+3n=5mn | B. | 2a•3a=6a | C. | (a2)3=a5 | D. | a6÷a2=a4 |
10.4月下旬某中学进行了初三体育考试,叶老师为了了解他所教的甲、乙两个班学生体育考试成绩哪一班比较整齐,通常需要知道两个班成绩的( )
| A. | 平均数 | B. | 众数 | C. | 方差 | D. | 频率分布 |
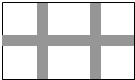 学校课外生物小组的试验园地是长20米宽15米的长方形.为了便于管理,现要在中间开辟一横两纵等宽的小道(如图),要使种植面积为252平方米,求小道的宽.
学校课外生物小组的试验园地是长20米宽15米的长方形.为了便于管理,现要在中间开辟一横两纵等宽的小道(如图),要使种植面积为252平方米,求小道的宽.