题目内容
8.(1)已知两点A(-3,m),B(n,4),若AB∥x轴,求m的值,并确定n的范围;(2)若点(5-a,a-3)在第一、三象限的角平分线上,求a的值.
分析 (1)根据平行x轴的直线上的点的纵坐标相等,可得m的值,根据A、B两点,可得n的范围;
(2)根据一三象限角平分线上的点的横坐标等于纵坐标,可得关于a的方程,根据解方程,可得答案.
解答 解:(1)两点A(-3,m),B(n,4),若AB∥x轴,得
m=4,n≠-3;
(2)由 点(5-a,a-3)在第一、三象限的角平分线上,得
5-a=a-3.
解得a=4.
点评 本题考查了坐标与图形的性质,利用了平行于x轴直线上的点的纵坐标相等,角平分线上的点的横坐标等于纵坐标.

练习册系列答案
相关题目
3.某超市从水果生产基地购进一批水果,运输过程中将会有10%的损耗,假如不计超市其他费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高( )
| A. | $\frac{2}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{7}$ | D. | $\frac{3}{10}$ |
20.若有一个n边形,其内角和大于它的外角和,则n的值至少为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
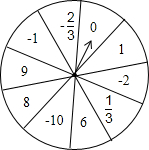 如图是小明和小颖共同设计的自由转动的十等分转盘,上面写有10个有理数.
如图是小明和小颖共同设计的自由转动的十等分转盘,上面写有10个有理数.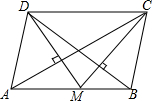 点M在平行四边形ABCD的边AB上,满足AM:MB=4:3,且DM和CM分别垂直于AC和BD.若BC=5cm,请问?ABCD的面积是多少cm2?
点M在平行四边形ABCD的边AB上,满足AM:MB=4:3,且DM和CM分别垂直于AC和BD.若BC=5cm,请问?ABCD的面积是多少cm2?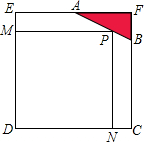 已知边长为4的正方形截取一个角后成为五边形ABCDE(如图),其中AF=2,BF=1.若在AB上有一点P使矩形MPND的面积最大,请你求出此时矩形MPND的边长DN、PN.
已知边长为4的正方形截取一个角后成为五边形ABCDE(如图),其中AF=2,BF=1.若在AB上有一点P使矩形MPND的面积最大,请你求出此时矩形MPND的边长DN、PN.