题目内容
16.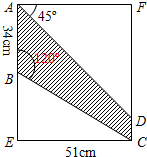 在2016首届合肥风筝文化节期间,某校丁周同学想在一个矩形材料中剪出如图阴影所示的图形,作为要制作的风筝的一个翅膀,请你根据图中的数据帮丁周同学计算出BE、CD的长度(精确到个位,$\sqrt{3}$≈1.7).
在2016首届合肥风筝文化节期间,某校丁周同学想在一个矩形材料中剪出如图阴影所示的图形,作为要制作的风筝的一个翅膀,请你根据图中的数据帮丁周同学计算出BE、CD的长度(精确到个位,$\sqrt{3}$≈1.7).
分析 解直角三角形求得BE,即可求得AE,根据矩形的性质和等腰直角三角形的性质得到DF的长,由CD=FC-FD,即可求得CD的长.
解答 解:∵∠ABC=120°,
∴∠EBC=180°-120°=60°,
在Rt△BCE中,CE=51,∠EBC=60°,
∴tan60°=$\frac{EC}{BE}$,
∴BE=$\frac{51}{tan60°}$=$\frac{51}{\sqrt{3}}$=17$\sqrt{3}$≈29cm;
在矩形ABCD中,由∠BAD=45°,得∠ADF=∠DAF=45°,
∴DF=AF=51,
∴FC=AE=34+29=63cm,
∴CD=FC-FD=63-51=12cm,
因此BE的长度约为29cm,CD的长度约为12cm.
点评 本题考查了直角三角形的应用,考查了在直角三角形中利用特殊角的三角函数求得三角形的边.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 如图,在梯形ABCD 中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒lcm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).
如图,在梯形ABCD 中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒lcm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).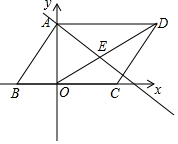 如图,平行四边形ABCD在直角坐标系中,tan∠ABC=$\frac{4}{3}$,AD=6,OA的长是方程x2-x-12=0的一个根,E是线段OD的中点.
如图,平行四边形ABCD在直角坐标系中,tan∠ABC=$\frac{4}{3}$,AD=6,OA的长是方程x2-x-12=0的一个根,E是线段OD的中点.
 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).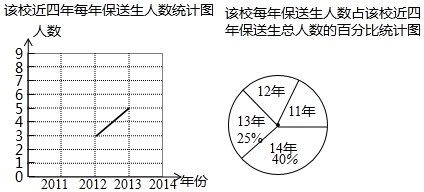
 如图,m∥n,等边△ABC的顶点B在直线n上,边AC交直线m于D,∠1=25°,则∠2的度数为35°.
如图,m∥n,等边△ABC的顶点B在直线n上,边AC交直线m于D,∠1=25°,则∠2的度数为35°.