题目内容
6.先化简,再求值:$\frac{{x}^{2}-8x+16}{{x}^{2}+2x}÷(\frac{12}{x+2}-x+2)+\frac{1}{x+4}$,其中x为方程x2+4x-3=0的根.分析 根据分式的加减法和除法可以化简题目中的式子,然后对x2+4x-3=0变形即可解答本题.
解答 解:$\frac{{x}^{2}-8x+16}{{x}^{2}+2x}÷(\frac{12}{x+2}-x+2)+\frac{1}{x+4}$
=$\frac{(x-4)^{2}}{x(x+2)}÷\frac{12-(x-2)(x+2)}{x+2}+\frac{1}{x+4}$
=$\frac{(x-4)^{2}}{x(x+2)}•\frac{x+2}{-(x+4)(x-4)}+\frac{1}{x+4}$
=$\frac{4-x}{x(x+4)}+\frac{1}{x+4}$
=$\frac{4-x+x}{x(x+4)}$
=$\frac{4}{{x}^{2}+4x}$,
∵x2+4x-3=0,
∴x2+4x=3,
∴原式=$\frac{4}{3}$.
点评 本题考查分式的化简求值、一元二次方程的解,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
相关题目
17.函数y=kx-k的图象可能是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN,AC=6,BD=8,求AM.
如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN,AC=6,BD=8,求AM. 将一副三角尺按如图所示的方式叠放(两条直角边重合),则∠α的度数是75°.
将一副三角尺按如图所示的方式叠放(两条直角边重合),则∠α的度数是75°.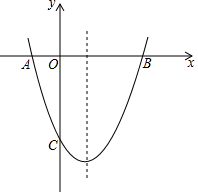 抛物线y=ax2+bx+c交x轴于A,B两点,交y轴于点C,已知抛物线的对称轴为x=1,点B的坐标为(3,0),点C的坐标为(0,-3)
抛物线y=ax2+bx+c交x轴于A,B两点,交y轴于点C,已知抛物线的对称轴为x=1,点B的坐标为(3,0),点C的坐标为(0,-3)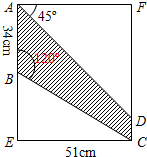 在2016首届合肥风筝文化节期间,某校丁周同学想在一个矩形材料中剪出如图阴影所示的图形,作为要制作的风筝的一个翅膀,请你根据图中的数据帮丁周同学计算出BE、CD的长度(精确到个位,$\sqrt{3}$≈1.7).
在2016首届合肥风筝文化节期间,某校丁周同学想在一个矩形材料中剪出如图阴影所示的图形,作为要制作的风筝的一个翅膀,请你根据图中的数据帮丁周同学计算出BE、CD的长度(精确到个位,$\sqrt{3}$≈1.7).