题目内容
17.在Rt△ABC中,∠C=90°,AB=10cm,BC=6cm,点M以2(单位:cm/s)的速度在线段AB上由点A向点B匀速运动,运动到点B时停止,过点M作MN⊥AB与三角形的直角边相交于点N,设运动时间为t(单位:s)(1)如图1,当点N在AC上时,用含t的代数式表示MN的长度;
(2)当Rt△ABC被MN分成面积1:2的两部分时,求t的值.

分析 (1)由勾股定理求出AC8cm,证明△ANM∽△ABC,得出$\frac{MN}{BC}=\frac{AM}{AC}$,求出MN=$\frac{3}{2}$t即可;
(2)求出△ABC的面积=$\frac{1}{2}$AC•BC=24(cm2),分情况讨论:
①当点N在AC上时,△AMN的面积=$\frac{1}{2}$AM•MN=$\frac{1}{2}$×2t×$\frac{3}{2}$t=$\frac{3}{2}$t2;(a)若$\frac{3}{2}$t2=$\frac{1}{3}$×24,求出t=$\frac{4\sqrt{3}}{3}$;(b)若$\frac{3}{2}$t2=$\frac{2}{3}$×24,求出t=$\frac{4\sqrt{6}}{3}$;
②当点N在BC上时,△BMN∽△BCA,求出MN=$\frac{40-8t}{3}$,得出△BMN的面积=$\frac{1}{2}$×(10-2t)×$\frac{40-8t}{3}$=$\frac{1}{3}$×24,解方程即可.
解答 解:(1)∵∠C=90°,AB=10cm,BC=6cm,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8cm,MN⊥AB,
∴∠AMN=90°=∠C,
又∵∠A=∠A,
∴△ANM∽△ABC,
∴$\frac{MN}{BC}=\frac{AM}{AC}$,即$\frac{MN}{6}=\frac{2t}{8}$,
解得:MN=$\frac{3}{2}$t;
(2)△ABC的面积=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×8×6=24(cm2),
分两种情况讨论:
①当点N在AC上时,△AMN的面积=$\frac{1}{2}$AM•MN=$\frac{1}{2}$×2t×$\frac{3}{2}$t=$\frac{3}{2}$t2;
(a)若$\frac{3}{2}$t2=$\frac{1}{3}$×24,
解得:t=±$\frac{4\sqrt{3}}{3}$(负值舍去),
∴t=$\frac{4\sqrt{3}}{3}$;
(b)若$\frac{3}{2}$t2=$\frac{2}{3}$×24,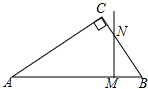
解得:t=±$\frac{4\sqrt{6}}{3}$(负值舍去),
∴t=$\frac{4\sqrt{6}}{3}$;
②当点N在BC上时,如图所示:
则△BMN∽△BCA,
∴$\frac{MN}{AC}=\frac{BM}{BC}$,
解得:MN=$\frac{40-8t}{3}$,
∴△BMN的面积=$\frac{1}{2}$×(10-2t)×$\frac{40-8t}{3}$=$\frac{1}{3}$×24,
解得:t=5±$\sqrt{3}$,
经检验,t=5+$\sqrt{3}$不合题意舍去,
∴t=5-$\sqrt{3}$;
综上所述:当Rt△ABC被MN分成面积1:2的两部分时,t的值为$\frac{4\sqrt{3}}{3}$或$\frac{4\sqrt{6}}{3}$或5-$\sqrt{3}$.
点评 本题考查了相似三角形的判定与性质、勾股定理、三角形面积的计算等知识;熟练掌握相似三角形的判定与性质,进行分类讨论是解决问题的关键.

 口算能手系列答案
口算能手系列答案 如图,AB为⊙O直径,已知圆周角∠BCD=30°,则∠ABD为( )
如图,AB为⊙O直径,已知圆周角∠BCD=30°,则∠ABD为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
| A. | 6,7,8 | B. | 12,13,5 | C. | 2,4,6 | D. | 3,4,6 |
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
| A. | 1 | B. | 3 | C. | 4 | D. | 5 |
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
 如图,CD是AB的垂直平分线,AC=1.6cm,BD=2.3cm,则四边形ACBD的周长为( )
如图,CD是AB的垂直平分线,AC=1.6cm,BD=2.3cm,则四边形ACBD的周长为( )| A. | 3.9cm | B. | 8.8cm | C. | 7.8cm | D. | 无法计算 |
 如图,在△ABC中,∠ABC=90°,∠C=30°,D在BC上,AD=DC.
如图,在△ABC中,∠ABC=90°,∠C=30°,D在BC上,AD=DC.