题目内容
13．计算（x+y-z）3n（z-x-y）2n（x-z+y）5n（n为正整数）的结果是（x+y-z）11n．分析 将z-x-y变形成-（x+y-z）化为同底数幂，根据同底数幂运算法则计算即可．
解答 解：∵n为正整数，∴2n是偶数；
则（x+y-z）3n（z-x-y）2n（x-z+y）5n=（x+y-z）3n[-（x+y-z）]2n（x+y-z）5n=（x+y-z）3n（x+y-z）2n（x+y-z）5n=（x+y-z）11n．
故答案为：（x+y-z）11n．
点评 本题主要考查同底数幂的乘法运算，将z-x-y变形成-（x+y-z）化为同底数幂是关键．
练习册系列答案
相关题目
如图是以△ABC的边AB为直径的半圆O，点C恰好在半圆上，过C作CD⊥AB交AB于D．已知cos∠ACD=$\frac{3}{5}$，BC=5，则AC的长为$\frac{20}{3}$．
如图所示，△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．若BC=10，则CF=$\frac{10}{3}$．
1．凸四边形ABCD中，AB=3，BC=4，CD=7，则AD边的取值范围为（ ）
| A． | 2＜AD＜7 | B． | 2＜AD＜13 | C． | 0＜AD＜14 | D． | 1＜AD＜13 |
5．已知$\frac{1}{a}$-$\frac{1}{b}$=2，则$\frac{ab}{2a+3ab-2b}$的值为（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | 1 | D． | -1 |
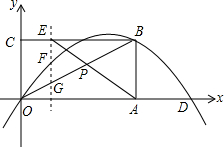如图，在平面直角坐标系xOy中，矩形OABC的边OA在x轴上，顶点B（4，2）在抛物线y=ax2+bx上，且抛物线交x轴于另一点D（6，0）．