题目内容
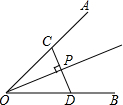 如图,P是∠AOB平分线上一点,CD⊥OP于F,并分别交OA、OB于CD,则CD( )P点到∠AOB两边距离之和.
如图,P是∠AOB平分线上一点,CD⊥OP于F,并分别交OA、OB于CD,则CD( )P点到∠AOB两边距离之和.| A、小于 | B、大于 |
| C、等于 | D、不能确定 |
考点:角平分线的性质,垂线段最短
专题:
分析:过P作PE⊥OA于E,PF⊥OB于F,则∠PED=∠PFD=90°,根据垂线段最短得出PC>PE,PD>PF,即可得出答案.
解答:解:
过P作PE⊥OA于E,PF⊥OB于F,
则∠PED=∠PFD=90°,
所以PC>PE,PD>PF,
∴PC+PD>PE+PF,
即CD大于P点到∠AOB两边距离之和,
故选B.

过P作PE⊥OA于E,PF⊥OB于F,
则∠PED=∠PFD=90°,
所以PC>PE,PD>PF,
∴PC+PD>PE+PF,
即CD大于P点到∠AOB两边距离之和,
故选B.
点评:本题考查了角平分线性质,垂线段最短的应用,解此题的关键是推出PD>PF,PC>PE.

练习册系列答案
相关题目
抛物线y=x2+4m与直线y=2(m+1)x(m为常数)( )
| A、没有交点 |
| B、只有一个交点 |
| C、有两个交点 |
| D、至少有一个交点 |
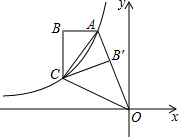 如图,双曲线y=
如图,双曲线y= 如图,AB是⊙O的直径,
如图,AB是⊙O的直径,