题目内容
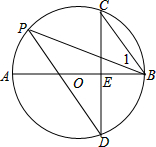 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C,
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C,(1)求证:CB∥PD;
(2)若BC=3,∠C=30°,求⊙O的直径.
考点:圆周角定理,垂径定理
专题:证明题
分析:(1)根据圆周角定理得∠P=∠C,而∠1=∠C,则∠1=∠P,于是根据平行线的判定即可得到CB∥PB;
(2)解:连结OC,如图,有(1)得∠1=∠P=30°,再根据垂径定理得到
=
,则利用圆周角定理得∠BOC=2∠P=60°,于是可判断△BOC为等边三角形,所以OB=BC=3,
易得⊙O的直径为6.
(2)解:连结OC,如图,有(1)得∠1=∠P=30°,再根据垂径定理得到
 |
| BC |
 |
| BD |
易得⊙O的直径为6.
解答:(1)证明:∵∠P=∠C,
而∠1=∠C,
∴∠1=∠P,
∴CB∥PB;
(2)解:连结OC,如图,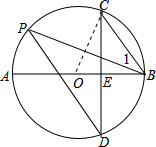
∵∠1=30°,
∴∠P=30°,
∵CD⊥AB,
∴
=
,
∴∠BOC=2∠P=60°,
∴△BOC为等边三角形,
∴OB=BC=3,
∴⊙O的直径为6.
而∠1=∠C,
∴∠1=∠P,
∴CB∥PB;
(2)解:连结OC,如图,

∵∠1=30°,
∴∠P=30°,
∵CD⊥AB,
∴
 |
| BC |
 |
| BD |
∴∠BOC=2∠P=60°,
∴△BOC为等边三角形,
∴OB=BC=3,
∴⊙O的直径为6.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
下列说法中,错误的是( )
| A、若两个三角形全等,则它们的面积相等 |
| B、若两个三角形的面积相等,则这两个三角形全等 |
| C、若两个三角形全等,则它们的周长相等 |
| D、若两个三角形的周长不相等,则这两个三角形不全等 |
 如图所示,E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.
如图所示,E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.