题目内容
如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形PQMN,使点Q落在线段AE上,点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.

(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形PQMN,使点Q落在线段AE上,点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.

考点:四边形综合题,全等三角形的判定与性质,勾股定理,相似三角形的判定与性质
专题:综合题
分析:(1)根据矩形的性质、轴对称的性质可得到AD=EC,AE=DC,即可证到△DEC≌△EDA(SSS);
(2)易证AF=CF,设DF=x,则有AF=4-x,然后在Rt△ADF中运用勾股定理就可求出DF的长;
(3)过点E作EH⊥AC于点H,交EH于点G,如图2,设EP=x,然后运用相似三角形的性质求出PQ、GH的值(用x的代数式表示),从而得到矩形PQMN的面积(用x的代数式表示),然后只需运用配方法就可解决问题.
(2)易证AF=CF,设DF=x,则有AF=4-x,然后在Rt△ADF中运用勾股定理就可求出DF的长;
(3)过点E作EH⊥AC于点H,交EH于点G,如图2,设EP=x,然后运用相似三角形的性质求出PQ、GH的值(用x的代数式表示),从而得到矩形PQMN的面积(用x的代数式表示),然后只需运用配方法就可解决问题.
解答:(1)证明:∵四边形ABCD是矩形,
∴AD=BC,AB=DC.
由折叠可得:EC=BC,AE=AB,
∴AD=EC,AE=DC.
在△DEC和△EDA中,
,
∴△DEC≌△EDA.
(2)解:∵四边形ABCD是矩形,
∴∠DCA=∠BAC.
由折叠可得∠EAC=∠BAC,
∴∠EAC=∠DCA,
∴AF=CF.
设DF=x,则AF=CF=DC-DF=AB-DF=4-x.
在Rt△ADF中,
∵AD2+DF2=AF2,
∴32+x2=(4-x)2,
解得:x=
.
∴DF的值为
.
(3)解:过点E作EH⊥AC于点H,交EH于点G,设EP=x,如图2,
则有EG⊥PQ.
在Rt△AEC中,
∵AE=AB=4,EC=BC=AD=3,
∴AC=5.
∵S△AEC=
AE•EC=
AC•EH,
∴EH=
=
=
.
∵四边形PQMN是矩形,
∴PQ∥MN,
∴△EPQ∽△ECA,
∴
=
=
,
∴
=
=
,
∴EG=
x,PQ=
x,
∴GH=EH-EG=
-
x,
∴S矩形PQMN=PQ•GH
=
x•(
-
x)
=-
x2+4x
=-
(x2-3x)
=-
[(x-
)2-
]
=-
(x-
)2+3.
∵-
<0,
∴当x=
时,S矩形PQMN最大,最大值为3.
∴当线段PE的长为
时,矩形PQMN的面积最大,最大值为3.

∴AD=BC,AB=DC.
由折叠可得:EC=BC,AE=AB,
∴AD=EC,AE=DC.
在△DEC和△EDA中,
|
∴△DEC≌△EDA.
(2)解:∵四边形ABCD是矩形,
∴∠DCA=∠BAC.
由折叠可得∠EAC=∠BAC,
∴∠EAC=∠DCA,
∴AF=CF.
设DF=x,则AF=CF=DC-DF=AB-DF=4-x.
在Rt△ADF中,
∵AD2+DF2=AF2,
∴32+x2=(4-x)2,
解得:x=
| 7 |
| 8 |
∴DF的值为
| 7 |
| 8 |
(3)解:过点E作EH⊥AC于点H,交EH于点G,设EP=x,如图2,
则有EG⊥PQ.
在Rt△AEC中,
∵AE=AB=4,EC=BC=AD=3,
∴AC=5.

∵S△AEC=
| 1 |
| 2 |
| 1 |
| 2 |
∴EH=
| AE•EC |
| AC |
| 4×3 |
| 5 |
| 12 |
| 5 |
∵四边形PQMN是矩形,
∴PQ∥MN,
∴△EPQ∽△ECA,
∴
| EG |
| EH |
| PQ |
| AC |
| EP |
| EC |
∴
| EG | ||
|
| PQ |
| 5 |
| x |
| 3 |
∴EG=
| 4 |
| 5 |
| 5 |
| 3 |
∴GH=EH-EG=
| 12 |
| 5 |
| 4 |
| 5 |
∴S矩形PQMN=PQ•GH
=
| 5 |
| 3 |
| 12 |
| 5 |
| 4 |
| 5 |
=-
| 4 |
| 3 |
=-
| 4 |
| 3 |
=-
| 4 |
| 3 |
| 3 |
| 2 |
| 9 |
| 4 |
=-
| 4 |
| 3 |
| 3 |
| 2 |
∵-
| 4 |
| 3 |
∴当x=
| 3 |
| 2 |
∴当线段PE的长为
| 3 |
| 2 |
点评:本题主要考查了矩形的性质、全等三角形的判定与性质、相似三角形的判定与性质、二次函数的最值、勾股定理、等腰三角形的判定、轴对称的性质等知识,综合性比较强.而运用相似三角形的性质及配方法是解决第(3)小题的关键.

练习册系列答案
相关题目
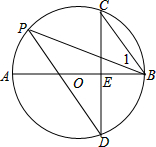 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C,
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C,