题目内容
观察下面三行数:
①-2,4,-8,16,-32,64,…
②0,6,-6,18,-30,66,…
③-1,2,-4,8,-16,32,…
(1)第①行听第10个数是 ;
(2)观察第①、②两行数的关系,则第②行中第n个数是 ;
(3)观察第①、③两行数的关系,则第③行中第n个数是 .
①-2,4,-8,16,-32,64,…
②0,6,-6,18,-30,66,…
③-1,2,-4,8,-16,32,…
(1)第①行听第10个数是
(2)观察第①、②两行数的关系,则第②行中第n个数是
(3)观察第①、③两行数的关系,则第③行中第n个数是
考点:规律型:数字的变化类
专题:
分析:(1)观察可看出第①行的数分别是-2的1次方,2次方,3次方,4次方…且奇数项是负数,偶数项是正数,用式子表示规律为:(-2)n;
(2)观察可知,第②行数是第①行数对应加2;
(3)第③行数是第①行数对应乘
,第三行数的规律为:
(-2)n.
(2)观察可知,第②行数是第①行数对应加2;
(3)第③行数是第①行数对应乘
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:1)第①行听第10个数是(-2)10;
(2)观察第①、②两行数的关系,则第②行中第n个数是(-2)n+2;
(3)观察第①、③两行数的关系,则第③行中第n个数
(-2)n.
故答案为:(-2)10;(-2)n+2;
(-2)n.
(2)观察第①、②两行数的关系,则第②行中第n个数是(-2)n+2;
(3)观察第①、③两行数的关系,则第③行中第n个数
| 1 |
| 2 |
故答案为:(-2)10;(-2)n+2;
| 1 |
| 2 |
点评:此题主要考查数字的变化规律,解答此类题对给出的条件仔细观察从而找出规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各式从左边到右边的变形是因式分解的是( )
| A、(a+1)(a-1)=a2-1 |
| B、a2-2a+1=(a-2+1) |
| C、ma+mb+na+nb=m(a+b)+n(a+b) |
| D、x2-y2=(x-y)(x+y) |
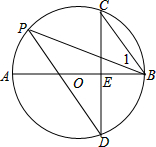 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C,
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C,